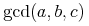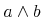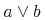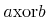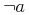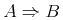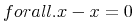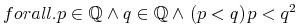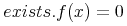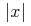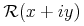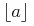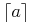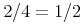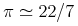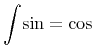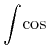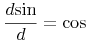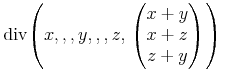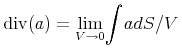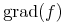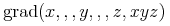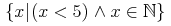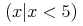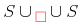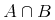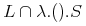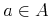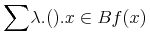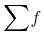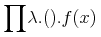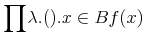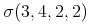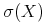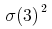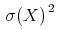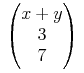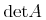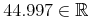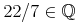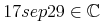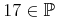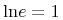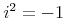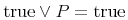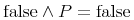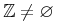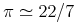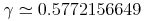4.1 Introduction
In MathML 3, content markup is divided into two subsets "Strict"- and "Pragmatic" Content MathML. The first subset uses a minimal set of elements representing the meaning of a mathematical expression in a uniform structure, while the second one tries to strike a pragmatic balance between verbosity and formality. Both forms of content expressions are legitimate and have their role in representing mathematics. Strict Content MathML is canonical in a sense and simplifies the implementation of content MathML processors and the comparison of content expressions and Pragmatic Content MathML is much simpler and more intuitive for humans to understand, read, and write.
Strict content MathML expressions can directly be given a formal semantics in terms of "OpenMath Objects" [OpenMath2004], and we interpret pragmatic content MathML expressions by specifying equivalent Strict variants, so that they inherit their semantics.
4.2 Strict Content MathML
4.2.1 The structure of MathML Content Expressions
MathML content encoding is based on the concept of an expression tree built up from
-
basic expressions, i.e. Numbers, Symbols, and Identifiers
-
derived expressions, i.e. function applications and binding expressions, and
As a general rule, the terminal nodes in the tree represent basic mathematical objects such as numbers, variables, arithmetic operations and so on. The internal nodes in the tree generally represent some kind of function application or other mathematical construction that builds up a compound object. Function application provides the most important example; an internal node might represent the application of a function to several arguments, which are themselves represented by the terminal nodes underneath the internal node.
This section provides the basic XML Encoding of content MathML expression trees. General usage and the mechanism used to associate mathematical meaning with symbols are provided here. [mathml3cds] provides a complete listing of the specific Content MathML symbols defined by this specification along with full reference information including attributes, syntax, and examples. It also describes the intended semantics of those symbols and suggests default renderings. The rules for using presentation markup within content markup are explained in Section 5.3.1 Presentation Markup in Content Markup.
4.2.2 Encoding OpenMath Objects
Strict Content MathML is designed to be and XML encoding of OpenMath Objects (see [OpenMath2004]), which constitute the semantics of strict content MathML expressions. The table below gives an element-by-element correspondence between the OpenMath XML encoding of OpenMath objects and strict content MathML.
| strict Content MathML | OpenMath |
|---|---|
cn |
OMI, OMF |
csymbol |
OMS |
ci |
OMV |
apply |
OMA |
bind |
OMBIND |
bvar |
OMBVAR |
share |
OMR |
semantics |
OMATTR, OMATP |
annotation,
annotation-xml |
OMFOREIGN |
error |
OME |
4.2.3 Numbers (cn)
| Editorial note: MiKo | |
| Some of the original parts of this section has been moved to the section as pragmatic MathML, it is rather new and might change at any moment as the discussion in the Math WG progresses. | |
The cn element is the MathML element used to represent numbers. Strict
content MathML supports integers, real numbers, double precision floating point
numbers.Pragmatic content MathML also
supports representation of real numbers by e-notation, rational numbers and complex
numbers.
Where it makes sense, the base in which the number is written can be specified. The
content of a cn element is PCDATA. The permissible attributes on the
cn are:
| Name | Values | Default |
|---|---|---|
type |
"integer" | "real" | "double" | real |
base |
number | 10 |
hex |
hex |
The type attribute specifies which kind of number is represented in the
cn element. Unless otherwise specified, the default "real" is
used. The attribute base is used to specify how the content is to be parsed.
The attribute value is a base 10 positive integer giving the value of base in which the
PCDATA is to be interpreted. The base attribute should only be used
on elements with type "integer" or "real". Its use on
cn elements of other type is deprecated. The default value for base
is "10".
Each data type implies that the content be of a certain form, as detailed below.
- integer
-
An integer is represented by an optional sign followed by a string of one or more "digits". How a "digit" is interpreted depends on the
baseattribute. Ifbaseis present, it specifies the base for the digit encoding, and it specifies it base 10. Thusbase='16' specifies a hexadecimal encoding.When
base> 10, letters are used in alphabetical order as digits. For example,<cn base="16">7FE0</cn>
encodes the number written as 32736 in base ten.
When
base> 36, some integers cannot be represented using numbers and letters alone and it is up to the application what additional characters (if any) may be used for digits. For example,<cn base="1000">10F</cn>
represents the number written in base 10 as 1,000,015. However, the number written in base 10 as 1,000,037 cannot be represented using letters and numbers alone when
baseis 1000. - real
-
A real number is presented in radix notation. Radix notation consists of an optional sign ("+" or "-") followed by a string of digits possibly separated into an integer and a fractional part by a "decimal point". Some examples are 0.3, 1, and -31.56. If a different
baseis specified, then the digits are interpreted as being digits computed to that base (in the same was as described for type "integer"). - double
-
This type is used to mark up those double-precision floating point numbers that can be represented in the IEEE 754 standard. This includes a subset of the (mathematical) real numbers, negative zero, positive and negative real infinity and a set of "not a number" values.
The content of a
cnelement may be PCDATA (representing numeric values as described below), ainfinitysymbol (representing positive real infinity), aminfinitysymbol (representing negative real infinity) or anotanumberelement.Editorial note: Miko Stephen is postulating an mininfinitysymbol here, but we do not have one yet.Editorial note: MiKo We have decided in the F2F that we are adding a hexattribute to allow the encoding of IEEE NaNs. David will write something about this here. Furthermore, we should not forget to add the hex attribute on thenotanumberandinfinityelements in pragmatic content MathML.If the content is PCDATA, it is interpreted as a real number in scientific notation. The number then has one or two parts, a significand and possibly an exponent. The significand has the format of a base 10 real number, as described above. The exponent (if present) has the format of a base 10 integer as described above. If the exponent is not present, it is taken to have the value 0. The value of the number is then that of the significand times ten to the power of the exponent.
A special case of PCDATA content is recognized. If a number of the above form has a negative sign and all digits of the significand are zero, then it is taken to be a negative zero in the sense of the IEEE 754 standard.
4.2.4 Symbols and Identifiers
The notion of constructing a general expression tree is essentially that of applying an operator to sub-objects. For example, the sum "x+y" can be thought of as an application of the addition operator to two arguments x and y. And the expression "cos(π)" as the application of the cosine function to the number π.
In Content MathML, elements are used for operators and functions to capture the
crucial semantic distinction between the function itself and the expression
resulting from applying that function to zero or more arguments. This is addressed
by making the functions self-contained objects with their own properties and
providing an explicit apply construct corresponding to function
application. We will consider the apply construct in the next section.
In a sum expression "x+y" above, x and y typically taken to be "variables", since they have properties, but no fixed value, whereas the addition function is a "constant" or "symbol" as it denotes a specific function, which is defined somewhere externally. (Note that "symbol" is used here in the abstract sense and has no connection with any presentation of the construct on screen or paper).
4.2.4.1 Content Identifiers (ci)
Strict content MathML uses the ci element (for "content
identifier") to construct a variable, or an identifier that is not a
symbol. Its PCDATA content is interpreted as a name that identifies
it. Two variables are considered equal, iff their names are in the respective
scope (see Section 4.2.6 Bindings and Bound Variables (bind) for a discussion). A type
attribute indicates the type of object the symbol represents. Typically,
ci represents a real scalar, but no default is specified.
| Name | values | default |
|---|---|---|
| type | string | unspecified |
| name | string | unspecified |
| name | string | unspecified |
4.2.4.2 Content Symbols (csymbol)
Due to the nature of mathematics the meaning of the mathematical expressions must
be extensible. The key to extensibility is the ability of the user to define new
functions and other symbols to expand the terrain of mathematical discourse. The
csymbol element is used represent a "symbol" in much the same
way that ci is used to construct a variable. The difference is that
csymbol should refer to some mathematically defined concept with an
external definition referenced via the content dictionary attributes, whereas
ci is used for identifiers that are essentially "local" to the
MathML expression.
In MathML 3, external definitions are grouped in Content Dictionaries (structured documents for the definition of mathematical concepts; see [OpenMath2004] and [mathml3cds]).
We need three bits of information to fully identify a symbol: a symbol
name, a Content Dictionary name, and (optionally) a
Content Dictionary base URI, which we encode in the textual content
(which is the symbol name) and two attributes of the csymbol element:
cd and cdbase. The Content Dictionary is the location of the
declaration of the symbol, consisting of a name and, optionally, a unique prefix
called a cdbase which is used to disambiguate multiple Content
Dictionaries of the same name. There are multiple encodings for content
dictionaries, this referencing scheme does not distinguish between them. If a
symbol does not have an explicit cdbase attribute, then it inherits its
cdbase from the first ancestor in the XML tree with one, should such an
element exist. In this document we have tended to omit the cdbase for
brevity.
| Name | values | default |
|---|---|---|
| cdbase | URI | inherited |
| cd | NCName | required |
| Editorial note: MiKo | |
| need to fix the default URI here | |
| Issue default_cd | wiki (member only) |
|---|---|
Current CD default for csymbol |
|
|
We might make the |
|
| Resolution | None recorded |
There are other properties of the symbol that are not explicit in these fields but whose values may be obtained by inspecting the Content Dictionary specified. These include the symbol definition, formal properties and examples and, optionally, a Role which is a restriction on where the symbol may appear in a MathML expression tree. The possible roles are described in Chapter 8 MathML3 Content Dictionaries.
<csymbol cdbase="http://www.example.com" cd="VectorCalculus">Christoffel</csymbol>
For backwards compatibility with MathML2 and to facilitate the use of MathML
within a URI-based framework (such as RDF [rdf] or the Semantic
Web), the csymbol content together with the values of the cd
and cdbase attributes can be combined in the definitionURL
attribute: we provide the following scheme for constructing a canonical URI for an
MathML Symbol, which can be given in the definitionURL attribute.
URI =cdbase-value+ '/' +cd-value+ '#' +content
In the case of the Christoffel symbol above this would be the URI
http://www.example.com/VectorCalculus#Christoffel
For backwards compatibility with MathML2, we do not require that the
definitionURL point to a content dictionary. But if the URL in this
attribute is of the form above, it will be interpreted as the canonical URL of a
MathML symbol. So the representation above would be equivalent to the one below:
<csymbol definitionURL="http://www.example.com/VectorCalculus">Christoffel</csymbol>
| Issue MathML_CDs_URI | wiki (member only) |
|---|---|
| What is the official URI for MathMLCDs | |
|
We still have to fix this. Maybe it should correspond to the final resting place for CDs. |
|
| Resolution | None recorded |
| Issue definitionURL_encoding | wiki (member only) ISSUE-17 (member only) |
|---|---|
URI encoding of cdbase/cd/name triplet
|
|
|
The URI encoding of the triplet we propose here does not work (not yet for
MathMLCDs and not at all for OpenMath2 CDs). The URI reference proposed uses a bare
name pointer |
|
| Resolution | None recorded |
| Issue cdbase-default | wiki (member only) ISSUE-13 (member only) |
|---|---|
| cdbase default value | |
|
For the inheritance mechanism to be complete, it would make sense to define a
default cdbase attribute value, e.g. at the math element. We'd support
expressions ignorant of cdbase as they all are thus far. Something such as
|
|
| Resolution | None recorded |
4.2.5 Function Application (apply)
The most fundamental way of building a compound object in mathematics is by applying a function or an operator to some arguments. MathML supplies an infrastructure to represent this in expression trees, which we will present in this section.
An apply element is used to build an expression tree that represents the
result of applying a function or operator to its arguments. The tree corresponds to
a complete mathematical expression. Roughly speaking, this means a piece of
mathematics that could be surrounded by parentheses or "logical
brackets" without changing its meaning.
| Name | values | default |
|---|---|---|
| cdbase | URI | inherited |
For example, (x + y) might be encoded as
<apply><csymbol cd="arith1">plus</csymbol><ci>x</ci><ci>y</ci></apply>
The opening and closing tags of apply specify exactly the scope of any
operator or function. The most typical way of using apply is simple and
recursive. Symbolically, the content model can be described as:
<apply> op a b </apply>
where the operands a and b are MathML
expression trees themselves, and op is a MathML expression tree that
represents an operator or function. Note that apply constructs can be
nested to arbitrary depth.
An apply may in principle have any number of operands:
<apply> op a b [c...] </apply>
For example, (x + y + z) can be encoded as
<apply> <csymbol cd="arith1">plus</csymbol> <ci>x</ci> <ci>y</ci> <ci>z</ci> </apply>
Mathematical expressions involving a mixture of operations result in nested
occurrences of apply. For example, a x + b
would be encoded as
<apply><csymbol cd="arith1">plus</csymbol>
<apply><csymbol cd="arith1">times</csymbol>
<ci>a</ci>
<ci>x</ci>
</apply>
<ci>b</ci>
</apply>There is no need to introduce parentheses or to resort to operator precedence in
order to parse the expression correctly. The apply tags provide the proper
grouping for the re-use of the expressions within other constructs. Any expression
enclosed by an apply element is viewed as a single coherent object.
An expression such as (F+G)(x) might be a product, as in
<apply><csymbol cd="arith1">times</csymbol>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>F</ci>
<ci>G</ci>
</apply>
<ci>x</ci>
</apply>or it might indicate the application of the function F + G to the argument x. This is indicated by constructing the sum
<apply><csymbol cd="arith1">plus</csymbol><ci>F</ci><ci>G</ci></apply>
and applying it to the argument x as in
<apply>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>F</ci>
<ci>G</ci>
</apply>
<ci>x</ci>
</apply>Both the function and the arguments may be simple identifiers or more complicated expressions.
The apply element is conceptually necessary in order to distinguish
between a function or operator, and an instance of its use. The expression
constructed by applying a function to 0 or more arguments is always an element from
the codomain of the function. Proper usage depends on the operator that is being
applied. For example, the plus operator may have zero or more arguments,
while the minus operator requires one or two arguments to be properly
formed.
If the object being applied as a function is not already one of the elements
known to be a function (such as sin or plus) then it is treated as
if it were a function.
4.2.6 Bindings and Bound Variables (bind)
Some complex mathematical objects are constructed by the use of bound variables. For instance the integration variables in an integral expression is one.
4.2.6.1 Bindings
Such expressions are represented as MathML expression trees using the
bind element. Its first child is a MathML expression that represents a
binding operator (the integral operator in our example). This can be followed by a
non-empty list of bvar elements for the bound variables, and the
body of the binding, it is another content MathML expression.
| Name | values | default |
|---|---|---|
| cdbase | URI | inherited |
4.2.6.2 Bound Variables
The bvar element is a special qualifier element that is used to denote
the bound variable of a binding expression, e.g. in sums, products, and quantifiers
or user defined functions.
| Name | values | default |
|---|---|---|
| cdbase | URI | inherited |
Bound variables are identified by comparing the XML information sets of the
ci content after first carrying out XML space normalization. Such
identification can be made explicit by placing an id on the ci
element in the bvar element and referring to it using the name
attribute on all other instances. An example of this approach is
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci id="var-x">x</ci></bvar>
<apply>
<csymbol cd="relation1">lt</csymbol>
<ci name="var-x">x</ci>
<cn>1</cn>
</apply>
</bind>
This id based approach is especially helpful when constructions
involving bound variables are nested.
It can be necessary to associate additional information with a bound variable
one or more instances of it. The information might be something like a detailed
mathematical type, an alternative presentation or encoding or a domain of
application. Such associations are accomplished in the standard way by replacing a
ci element (even inside the bvar element) by a semantics
element containing both it and the additional information. Recognition of and
instance of the bound variable is still based on the actual ci elements
and not the semantics elements or anything else they may contain. The
id based approach outlined above may still be used.
4.2.6.3 Examples
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">eq</csymbol>
<apply><csymbol cd="arith1">minus</csymbol><ci>x</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</bind><bind>
<csymbol cd="calculus1">int</csymbol>
<bvar><ci id="var_x">x</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol>
<ci definitionURL="#var_x"><mi>x</mi></ci>
<cn>7</cn>
</apply>
</bind>| Editorial note: MiKo | |
| We need to say something about alpha-conversion here for OpenMath compatibility. | |
4.2.7 Structure Sharing (share)
To conserve space, MathML expression trees can make use of structure sharing
4.2.7.1 The share element
This element has an href attribute whose value is the value of a URI
referencing an id attribute of a MathML expression tree. When building the
MathML expression tree, the share element is replaced by a copy of the MathML
expression tree referenced by the href attribute. Note that this copy is
structurally equal, but not identical to the element referenced. The
values of the share will often be relative URI references, in which case they
are resolved using the base URI of the document containing the share element.
| Name | values | default |
|---|---|---|
| href | URI |
For instance, the mathematical object f(f(f(a,a),f(a,a)),f(a,a),f(a,a)) can be encoded as either one of the following representations (and some intermediate versions as well).
<math> <math>
<apply> <apply>
<ci>f</ci> <ci>f</ci>
<apply> <apply id="t1">
<ci>f</ci> <ci>f</ci>
<apply> <apply id="t11">
<ci>f</ci> <ci>f</ci>
<ci>a</ci> <ci>a</ci>
<ci>a</ci> <ci>a</ci>
</apply> </apply>
<apply> <share href="#t11"/>
<ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
</apply> </apply>
<apply> <share href="#t1"/>
<ci>f</ci>
<apply>
<ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<apply>
<ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
</apply>
</apply>
</math> </math>4.2.7.2 An Acyclicity Constraint
We say that an element dominates all its children and all elements they dominate. An
share element dominates its target, i.e. the element that carries the
id attribute pointed to by the href attribute. For instance in the
representation above the apply element with id="t1" and also the
second share dominate the apply element with id="t11".
The occurrences of the share element must obey the following global
acyclicity constraint: An element may not dominate itself. For instance the
following representation violates this constraint:
<apply id="foo">
<csymbol cd="arith1">plus</csymbol>
<cn>1</cn>
<apply>
<csymbol cd="arith1">plus</csymbol>
<cn>1</cn>
<share href="#foo"/>
</apply>
</apply>Here, the apply element with id="foo" dominates its third child,
which dominates the share element, which dominates its target: the element with
id="foo". So by transitivity, this element dominates itself, and by the
acyclicity constraint, it is not an MathML expression tree. Even though it could be given
the interpretation of the continued fraction
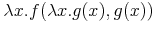 this would correspond to an infinite tree of applications, which is not admitted by
Content MathML
this would correspond to an infinite tree of applications, which is not admitted by
Content MathML
Note that the acyclicity constraints is not restricted to such simple cases, as the following example shows:
<apply id="bar"> <apply id="baz">
<csymbol cd="arith1">plus</csymbol> <csymbol cd="arith1">plus</csymbol>
<cn>1</cn> <cn>1</cn>
<share href="#baz"/> <share href="#bar"/>
</apply> </apply>
Here, the apply with id="bar" dominates its third child, the
share with href="#baz", which dominates its target apply
with id="baz", which in turn dominates its third child, the share
with href="#bar", this finally dominates its target, the original
apply element with id="bar". So this pair of representations
violates the acyclicity constraint.
4.2.7.3 Structure Sharing and Binding
Note that the share element is a syntactic referencing mechanism:
an share element stands for the exact element it points to. In particular,
referencing does not interact with binding in a semantically intuitive way, since it
allows for variable capture. Consider for instance
<bind id="outer">
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply>
<ci>f</ci>
<bind id="inner">
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<share id="copy" href="#orig"/>
</bind>
<apply id="orig"><ci>g</ci><ci>X</ci></apply>
</apply>
</bind>
it represents the term 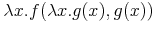 which has two sub-terms of the form
which has two sub-terms of the form 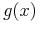 , one with
, one with id="orig"
(the one explicitly represented) and one with id="copy", represented by the
share element. In the original, the variable x is bound by the
outer bind element, and in the copy, the variable x is
bound by the inner bind element. We say that the inner bind
has captured the variable X.
It is well-known that variable capture does not conserve semantics. For instance, we
could use α-conversion to rename the inner occurrence of x into, say,
y arriving at the (same) object
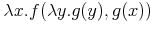 Using references that capture variables in this way can easily lead to representation
errors, and is not recommended.
Using references that capture variables in this way can easily lead to representation
errors, and is not recommended.
4.2.8 Attribution via semantics
Content elements can be adorned with additional information via the
semantics element. An attribution decorates a content MathML
expression with a sequence of one or more semantic annotations. MathML uses the
semantics element to wrap the annotated element and the
annotation-xml and annotation elements for representing the
annotations themselves. Each annotation has cdbase, cd, and
name attribute to specify the key, i.e. a symbol that
specifies the relation between the annotated object and the annotation; See Section 5.1 Semantic Annotations for details.
An annotation acts as either adornment annotation or as semantic annotation. When the key has role "attribution", then dropping the attribution is not harmful and preserves the semantics. When the key has role "semantic-attribution" then the attributed object is modified by the attribution and dropping changes semantics. If the attribute lacks the role specification then attribution is acting as adornment annotation.
An example of the use of an adornment attribution would be to indicate the color in which an content representation object A should be displayed, for example
<semantics>
A
<annotation-xml cd="display" name="color" encoding="MathML Presentation">
red
</annotation>
</semantics>Note red are arbitrary representations whereas the key is a symbol.
An example of the use of a semantic attribution would be to indicate the type of an object. For example the following expression associates with an identifier F the information that it represents an operator that takes real numbers as input and returns natural numbers as values (the absolute value function is an example of such a function).
<semantics>
<ci>F</ci>
<annotation-xml cd="types" name="typeof" encoding="MathML Content">
<apply>
<csymbol cd="types">funtype</csymbol>
<csymbol cd="setname1">integers</csymbol>
<csymbol cd="setname1">naturalnumbers</csymbol>
</apply>
<annotation-xml>
</semantics>
Here we have assumed the existence of a content dictionary types that
provides a key symbol typeof that specifies that the attributed
expression is of the type specified by the content MathML expression in the
annotation-xml element. The key is specified by the cd and
name attributes in the attribution-xml element. The
encoding attribute on the annotation-xml element specifies the
format of the XML data.
As such, the semantics element should be considered part of both
presentation MathML and content MathML. MathML considers a semantics element
(strict) content MathML, if and only if its first child is (strict) content MathML.
All MathML processors should process the semantics element, even if they only
process one of those subsets.
4.2.9 In Situ Error Markup
A content error expression is made up of a symbol and a sequence of zero or more MathML expression trees. This object has no direct mathematical meaning. Errors occur as the result of some treatment on an expression tree and are thus of real interest only when some sort of communication is taking place. Errors may occur inside other objects and also inside other errors.
| Name | values | default |
|---|---|---|
| cdbase | URI | inherited |
To encode an error caused by a division by zero, we would employ a
aritherror Content Dictionary with a DivisionByZero symbol
with role error we would use the following expression tree:
<cerror> <csymbol cd="aritherror">DivisionByZero</csymbol> <apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply> </cerror>
Note that the error should cover the smallest erroneous sub-expression so cerror
can be a sub-expression of a bigger one, e.g.
<apply><csymbol cd="relation1">eq</csymbol>
<cerror>
<csymbol cd="aritherror">DivisionByZero</csymbol>
<apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply>
</cerror>
<cn>0</cn>
</apply>If an application wishes to signal that the content MathML expressions it has received is invalid or is not well-formed then the offending data must be encoded as a string. For example:
<cerror> <csymbol cd="parser">invalid_XML</csymbol> <mtext> <<!--LESS-THAN SIGN-->apply><!--GREATER-THAN SIGN--><<!--LESS-THAN SIGN-->cos><!--GREATER-THAN SIGN--> <<!--LESS-THAN SIGN-->ci><!--GREATER-THAN SIGN-->v<<!--LESS-THAN SIGN-->/ci><!--GREATER-THAN SIGN--> <<!--LESS-THAN SIGN-->/apply><!--GREATER-THAN SIGN--> </mtext> </cerror>
Note that the < and > characters have been escaped as
is usual in an XML document.
4.3 Pragmatic Content MathML
Strict MathML3 content markup differs from earlier versions of MathML in that it has been regularized and based on the content dictionary model introduced by OpenMath [OpenMath2004]. MathML3 also supports MathML2-like markup as a pragmatic representation that is easier to read and more intuitive for humans. "Content MathML" without qualification consists of both types of markup together.
In the following we will discuss the general aspects of pragmatic Content MathML3 and indicate the equivalent strict Content MathML3 expressions. Thus the "pragmatic content MathML" representations inherit the meaning from their strict counterparts. As pragmatic Content MathML is not as regular as strict Content MathML and the mapping from the former to the latter is not regular either, the particulars will be covered in this section.
| Editorial note: MiKo | |
| This part of the specification is still under development and should not be considered as final. In particular, the description of the pragmatic-vs-strict correspondence is still somewhat under-defined and should only be considered as an indication of the intended relation. We anticipate that we may have to give normative specification of the relation as a XSLT style sheet that converts pragmatic content MathML expressions to strict content MathML expressions. Such a style sheet is under development at http://svn.openmath.org/OpenMath3/xsl/cmml2om.xsl (actually it transforms pragmatic content MathML to OpenMath, but this is equivalent, and can be transformed to strict content MathML via http://svn.openmath.org/OpenMath3/xsl/om2mml.xsl. | |
4.3.1 Pragmatic Numbers (cn)
| Editorial note: MiKo | |
| This section has been extracted from the section as pragmatic MathML, it is rather new and might change at any moment as the discussion in the Math WG progresses. | |
In pragmatic content MathML the cn allows additional values for the
type attribute element for supporting e-notations for real numbers, rational
numbers and complex numbers. Where it makes sense, the base in which the number is
written can be specified. For most numeric values, the content of a cn element
should be either PCDATA or other cn elements.
The permissible attributes on the cn are:
| Name | Values | Default |
|---|---|---|
type |
"e-notation," | "rational" | "complex-cartesian" | "complex-polar" | real |
base |
number | 10 |
Each data type implies that the content be of a certain form, as detailed below.
- e-notation
-
A real number may be presented in scientific notation using this type. Such numbers have two parts (a significand and an exponent) separated by a
<sep/>element. The first part is a real number, while the second part is an integer exponent indicating a power of the base. For example, 12.3<sep/>5 represents 12.3 times 105. The default presentation of this example is 12.3e5. In strict content MathML, we can just use thecnwith "double" if it is in the range of IEEE floats:<cn type="e-notation">12.3<sep/>5</cn>
Strict MathML equivlalent
<cn type="double">12.3e5</cn>
and we use a construction with bigfloat symbol from the bigfloat1 content dictionary.
<cn type="e-notation">12.3<sep/>5</cn>
Strict MathML equivlalent
<apply> <csymbol cd="bigfloat1">bigfloat</csymbol> <cn type="real">12.3</cn> <cn type="integer">10</cn> <cn type="integer">5</cn> </apply> - rational
-
A rational number is given as two integers giving the numerator and denominator of a quotient. These themselves can either be given as nested
cnelements or as PCDATA separated by<sep/>. In strict content MathML we use a construction with the rational symbol from the nums1 content dictionary.<cn type="rational">3<sep/>5</cn>
Strict MathML equivlalent
<apply> <csymbol cd="num1">rational</csymbol> <cn type="integer">3</cn> <cn type="integer">5</cn> </apply>If a
baseis present, it specifies the base used for the digit encoding of both integers.<cn type="rational" base="16">3<sep/>5</cn>
Strict MathML equivlalent
<apply> <csymbol cd="num1">rational</csymbol> <cn type="integer" base="16">3</cn> <cn type="integer" base="16">5</cn> </apply> - complex-cartesian
-
A complex cartesian number is given as two numbers giving the real and imaginary parts. These should themselves be given as nested
cnelements or as PCDATA separated by a<sep/>element. In strict content MathML we represent this using the complex_cartesian element from the complex1 content dictionary.<cn type="complex-cartesian">3.5<sep/>1.2</cn>
Strict MathML equivlalent
<apply> <csymbol cd="complex1">complex-cartesian</csymbol> <cn>3.5</cn> <cn>1.2</cn> </apply> - complex-polar
-
A complex polar number is given as two numbers giving the magnitude and angle. These should themselves be given as nested
cnelements or as PCDATA separated by a<sep/>element. In strict content MathML we represent this using the complex_polar element from the complex1 content dictionary.<cn type="complex-polar">3.5<sep/>1.2</cn>
Strict MathML equivlalent
<apply> <csymbol cd="complex1">complex-polar</csymbol> <cn>3.5</cn> <cn>1.2</cn> </apply> - constant
-
If the value
typeis "constant", then the content can be various Unicode representations of number constants. Several important constants such as π have been included explicitly in MathML 2 as empty elements. This use of thecnis discouraged in favor of the defined constants, or the use ofcsymbolelement with appropriate values for thecdandcdbaseattributes. For example, instead of using thepielement, an instance of<cn type="constant">π</cn>could be used. This should be interpreted as having the semantics of the mathematical constant Pi. The data for a constantcntag may be one of the following common constants:content intuition Symbol strict content MathML πThe usual π of trigonometry: approximately 3.141592653... pi <csymbol cd="nums1" name="pi"/> ⅇ(orⅇ)The base for natural logarithms: approximately 2.718281828... exponentiale <csymbol cd="nums1" name="e"/> ⅈ(orⅈ)Square root of -1 imaginaryi <csymbol cd="nums1" name="i"/> γEuler's constant: approximately 0.5772156649... eulergamma <csymbol cd="nums1" name="eulergamma"/> ∞(or&infty;)Infinity. Proper interpretation varies with context infinity <csymbol cd="nums1" name="infinity"/> &true;the logical constant true true <csymbol cd="logic1" name="true"/> &false;the logical constant false false <csymbol cd="logic1" name="false"/> &NotANumber;(or&NaN;)represents the result of an ill-defined floating point division notanumber <csymbol cd="nums1" name="notanumber"/>
4.3.2 Operator Elements
Pragmatic content MathML provides empty elements for the operators and functions
of the K-14 fragment of mathematics. For instance, the empty MathML element
<plus/> is equivalent to the element
<csymbol cdbase="http://w3.org/Math/CD" cd="arith1">plus</csymbol>
The set of elements is the same as the ones for MathML2 with few additions. In most cases, the names of the empty operator elements are the same as the symbol names defined in the MathML 3 content dictionaries. Note that the concepts of "MathML symbols" (defined in Section 4.2.4 Symbols and Identifiers) and "operator elements" are different. In particular not all symbols defined by the MathML 3 Content Dictionaries have corresponding operator elements in pragmatic Content MathML.
4.3.3 Pragmatic Elements with Attributes
Following MathML2, pragmatic content MathML allows to specialize the meaning of
some elements via attributes, usually the type attribute. Strict Content
MathML does not have this possibility, therefore these attributes are either passed to
the symbols as extra arguments in the apply or bind elements, or
MathML 3 adds new symbols for the non-default case to the respective content
dictionaries. These will normally not have corresponding operator elements (see
above).
For instance the closure interval element can be given by the
closure attribute. Thus the pragmatic content MathML expression
<apply><interval closure="open-closed"/><cn>0</cn><cn>1</cn></apply>
is equivalent to the strict content MathML expression
<apply><csymbol cd="interval1">interval-oc</csymbol><cn>0</cn><cn>1</cn></apply>
In MathML2, the definitionURL attribute could be used to modify the
meaning of an element to allow essentially the same notation to be re-used for a
discussion taking place in a different mathematical domain. This use of the attribute
is deprecated in MathML 3, in favor of using a
csymbol with cdbase and cd attributes that combine to
the same definitionURL attribute (see Section 4.2.4.2 Content Symbols (csymbol)).
4.3.4 Bindings with apply
Pragmatic content MathML allows to use the apply element instead of the
bind element to conserve backwards compatibility with MathML2. The mapping to
strict Content MathML applies two general principles here depending on the
operator. Where there is a binding operator in the content dictionaries, we use that
and only replace the apply tag with a bind tag. This is the case for
instance for the quantifiers: the pragmatic expression
<apply> <forall/> <bvar><ci>x</ci></bvar> <apply><geq/><ci>x</ci><ci>x</ci></apply> </apply>
is equivalent to the strict expression
<bind> <csymbol cd="logic1">forall</csymbol> <bvar><ci>x</ci></bvar> <apply><csymbol cd="relation1">geq</csymbol><ci>x</ci><ci>x</ci></apply> </bind>
This situation also obtains for the exists and lambda symbols.
Where binding operators are not available, we just convert the expression with the bound variable into a λ-expression. Usually we have to move any qualifiers into an argument. For instance for sums:
<apply> <sum/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
is equivalent to the strict expression.
<apply>
<sum/>
<apply>
<csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><power/><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>| Editorial note: MiKo | |
we should probably say here that we cannot expect alpha-conversion for
apply-with-bvar in contrast to the bind. An example for this is the
diff element where the bvar is not bound at all.
|
|
4.3.5 Container Markup
4.3.5.1 Container Markup for Constructor Symbols
Pragmatic content MathML provides an alternative representation for applications
of "constructor" symbols called "container
markup". Constructor symbols represent operators that construct mathematical
operators that construct a mathematical structure from a list of objects. This list
can be given by an explicit sequence of arguments or as an expression with a bound
variable. In pragmatic content MathML, we allow to write the argument list as
children to the element instead of having to append them as to the empty operator element
as children of an apply element.
For instance for the set constructor allow to write:
<set><ci>a</ci><ci>b</ci><ci>c</ci></set>
This is considered equivalent to the following strict content MathML expression.
<apply><csymbol cd="set1">set</csymbol><ci>a</ci><ci>b</ci><ci>c</ci></apply>
But the set constructor can also take a list that is given as an expression with a
bound variable in pragmatic Content MathML. Consider for instance the collection of
all intervals from 0 to x. Here we do not have a systematic correspondence,
since a symbol can only have one role. For the constructor symbols this is the role
application. Thus the pragmatic Content MathML expression
<set> <bvar><ci>x</ci></bvar> <interval><cn>0</cn><ci>x</ci></interval> </set>
has to be modeled by a
<apply>
<csymbol cd="set1">suchthat</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply>
<csymbol cd="interval1">interval</csymbol>
<cn>0</cn>
<ci>x</ci>
</apply>
</bind>
</apply>
Note that even though we have not made use of this here, the bound variable can be
qualified by any of the qualifier elements
condition, uplimit, lowlimit, domainofapplication,
and degree.
Note furthermore that container markup is restricted to the MathML2 elements
set, interval, list, matrix, matrixrow,
and vector.
4.3.5.2 Container Markup for Binding Constructors
The lambda element allows a kind of container markup for the
lambda symbol from the fns1 content dictionary. e.g.
<lambda><bvar><ci>x</ci></bvar><ci>x</ci></lambda>
but unlike the set element, which corresponds to a symbol with role
application, the role of the lambda symbol is
binding. Therefore the lambda element has to have at least one
bvar child followed by qualifiers (see below), followed by a content MathML
element. The strict Content MathML equivalent of the expression above is
<bind><csymbol cd="fns1">lambda</csymbol><bvar><ci>x</ci></bvar><ci>x</ci></bind>
4.3.5.3 Container Markup for Applicative Constructors
The piecewise, piece, and otherwise allow container
markup for the constructor symbols of the content dictionary piece1. Unlike the cases described above, these do not allow their arguments to
be represented as expressions with bound variables, so the strict-pragmatic
correspondence is very simple in this case. For instance the pragmatic Content MathML
representation of the absolute value function
<piecewise>
<piece>
<apply><minus/><ci>x</ci></apply>
<apply><lt/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<cn>0</cn>
<apply><eq/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<ci>x</ci>
<apply><gt/><ci>x</ci><cn>0</cn></apply>
</piece>
</piecewise>has the strict equivalent
<apply>
<csymbol cd="piece1">piecewise</csymbol>
<apply>
<csymbol cd="piece1">piece</csymbol>
<apply><csymbol cd="arith1">minus</csymbol><ci>x</ci></apply>
<apply><csymbol cd="arith1">lt</csymbol><ci>x</ci><cn>0</cn></apply>
</apply>
<apply>
<csymbol cd="piece1">piece</csymbol>
<cn>0</cn>
<apply><csymbol cd="arith1">eq</csymbol><ci>x</ci><cn>0</cn></apply>
</apply>
<apply>
<csymbol cd="piece1">piece</csymbol>
<ci>x</ci>
<apply><csymbol cd="arith1">gt</csymbol><ci>x</ci><cn>0</cn></apply>
</apply>
</apply>4.3.6 Symbols and Identifiers With Presentation MathML
In Pragmatic Content MathML, the ci and csymbol elements can
contain a general presentation construct (see Section 3.1.7 Summary of Presentation Elements), which
is used for rendering (see Section 4.5 Rendering of Content Elements). For example,
<csymbol cd="ContDiffFuncs"> <msup><mi>C</mi><mn>2</mn></msup> </csymbol>
encodes an atomic symbol that displays visually as C2 and that, for purposes of content, is treated as a single symbol representing the space of twice-differentiable continuous functions.
| Issue csymbol_pmathml_strict | wiki (member only) |
|---|---|
Strict equivalent for csymbol with pMathML content
|
|
|
What is the strict equivalent for the case of a |
|
| Resolution | None recorded |
A ci or csymbol element with Presentation MathML content is
equivalent to a semantics construction where the first child is a
ci whose content is the symbol or identifier name and whose second child is
an annotation-xml element with the MathML Presentation. For example the
Strict Content MathML equivalent to the example above would be
<semantics>
<csymbol cd="ContDiffFuncs">C2</csymbol>
<annotation-xml encoding="MathMLÂ Presentation">
<msup><mi>C</mi><mn>2</mn></msup>
</annotation-xml>
</semantics>In this situation, the name of the symbol name (which has to be a text string) can
be determined from the presentation MathML representation above by stripped off
elements. But this is not possible in general . Therefore pragmatic Content MathML
allows an additional name attribute on csymbol and ci
which allows to specify the name. It is highly advisable to supply name
attributes for symbols and identifiers that have presentation MathML content.
Alternatively, the definitionURL attribute can be used to associate a
name with with a ci element. See the discussion of bound variables (Section 4.2.6 Bindings and Bound Variables (bind)) for a discussion of an important instance of this. For example,
<ci name="c1"><msub><mi>c</mi><mn>1</mn></msub></ci>
encodes an atomic symbol that displays visually as c1 which, for purposes of content, is treated as a atomic concept representing a real number.
4.3.7 Elementary MathML Types on Operator and Container Elements
The ci element uses the type attribute to specify the basic type
of object that it represents. While any CDATA string is a valid type, the predefined
types include "integer", "rational",
"real", "complex", "complex-polar",
"complex-cartesian", "constant", "function"
and more generally, any of the names of the MathML container elements (e.g.
vector) or their type values. For a more advanced treatment of types, the
type attribute is inappropriate. Advanced types require significant
structure of their own (for example, vector(complex)) and are probably best constructed
as mathematical objects and then associated with a MathML expression through use of the
semantics element.
| Editorial note: MiKo | |
| Give the Strict equivalent here by techniques from the Types Note, but be careful what we eventually do with types. | |
4.3.8 Qualifiers for Bound Variables
In many situations, we want to specify range of bound variables, e.g. in definitive
integrals. A number of common mathematical constructions involve such restrictions,
either implicit in conventional notation, such as a bound variable, or thought of as
part of the operator rather than an argument, as is the case with the limits of a
definite integral. MathML 3 provides the optional qualifier elements
uplimit, lowlimit, domainofapplication, condition,
and degree as a pragmatic restriction mechanism.
4.3.8.1 Domain of Application
In pragmatic Content MathML the domainofapplication element may be used in
an apply element without bvar children to mark up the domain over
which a given function is being applied. In contrast to its use as a qualifier in the
bind element, the usage in the apply element only marks the argument
position. For instance, the integral of a function f over an arbitrary domain
C can be represented as
<apply><int/> <domainofapplication><ci>C</ci></domainofapplication> <ci>f</ci> </apply>
in Pragmatic Content MathML to mark the domain for the range argument of the definite integral. This expression is considered equivalent to
<apply><csymbol cd="calculus1">int</csymbol><ci>C</ci><ci>f</ci></apply>
4.3.8.2 Domain of Application in Bindings
The range of bound variables can be restricted by a domainofapplication in
pragmatic Content MathML. In strict Content MathML we usually represent such
restricted quantifiers with complex binding operators. For instance the expression
<apply><forall/> <bvar><ci>x</ci></bvar> <domainofapplication><ci type="set">D</ci></domainofapplication> <apply><ci>p</ci><ci>x</ci></apply> </apply>
is equivalent to the Strict Content MathML representation
<bind>
<apply>
<csymbol cd="quant1">every</csymbol>
<ci type="set">D</ci>
</apply>
<bvar><ci>x</ci></bvar>
<apply><ci>p</ci><ci>x</ci></apply>
</bind>
Note that the binding operator (the first child of the bind element) is not just a symbol, but a complex expression constructed by applying the every symbol to the set D.
4.3.8.3 degree
The degree element is a qualifier used by some MathML container elements to specify
that, for example, a bound variable is repeated several times, i.e. for the for the
"degree" or "order" of an operation. There are a number of
basic mathematical constructs that come in families, such as derivatives and
moments. Rather than introduce special elements for each of these families, pragmatic
MathML allows uses a single general construct, the degree element for this
concept of "order". This element is placed in the bvar element
before or after the variable itself.
For instance, in a derivative, the degree element indicates the order of
the derivative with respect to that variable.
<apply>
<diff/>
<bvar>
<ci>x</ci>
<degree><cn>2</cn></degree>
</bvar>
<apply><power/><ci>x</ci><cn>4</cn></apply>
</apply>Strict MathML equivlalent
<bind>
<apply><csymbol cd="calculus3">diff</csymbol><cn>2</cn></apply>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><cn>4</cn></apply>
</bind>| Editorial note: MiKo | |
| make sure that this is consistent with revised calculus3 | |
Note that the degree element is only allowed in the container representation. The strict representation
takes the degree as a regular argument as the second child of the apply or
bind element.
4.3.8.4 Upper and Lower Limits (uplimit and lowlimit)
The uplimit and lowlimit elements are pragmatic Content MathML
qualifiers that can be used to restrict the range of a bound variable to an interval,
e.g. in some integrals and sums. In strict content MathML, the
uplimit/lowlimit pairs can be expressed via the interval. For instance, we consider the Pragmatic Content MathML
representation
<apply><int/>
<bvar><ci> x </ci></bvar>
<lowlimit><ci>a</ci></lowlimit>
<uplimit><ci>b</ci></uplimit>
<apply><ci>f</ci><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="calculus1">defint</csymbol>
<apply><csymbol cd="interval1">interval</csymbol><ci>a</ci><ci>b</ci></apply>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><ci>f</ci><ci>x</ci></apply>
</bind>
</apply>| Editorial note: MiKo | |
| rework for calculus3 | |
If the lowlimit qualifier is missing, it is interpreted as negative infinity,
similarly, if uplimit is then it is interpreted as positive infinity.
4.3.8.5 Conditions (condition)
A condition element contains a single child that represents a truth
condition. Compound conditions are indicated by applying operators such as
and in the condition. Consider for instance the following representation of a
definite integral.
| Name | values | default |
|---|---|---|
| cdbase | URI | inherited |
For example
<bind>
<int/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/><ci>x</ci><ci>S</ci></apply>
</condition>
<apply><sin/><ci>x</ci></apply>
</bind>
Here the condition element restricts the bound variables to range over a set
S. In this special case, the strict counterpart is given by a construction
using the defint symbol:
<apply>
<csymbol cd="calculus1">defint</csymbol>
<ci>S</ci>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><sin/><ci>x</ci></apply>
</bind>
</apply>We will specify the special cases of the strict-to-pragmatic mapping with the
binding operators below. For the general case note that the binding operator can be a
csymbol element or even an identifier (ci). We treat these cases
differently. For the first case consider
<bind> <csymbol cd="foo">bar</csymbol> <bvar><ci>x</ci></bvar> <condition><apply><ci>P</ci><ci>x</ci></apply></condition> <apply><sin/><ci>x</ci></apply> </bind>
Restrictions via the condition element cannot be treated by complex
binding operators as the domainofapplication, uplimit,
lowlimit, and degree qualifiers in the strict-to-pragmatic mapping
since it contains the bound variable, which would be placed outside the scope of
alpha-renaming. Therefore we need to place the content of the condition
element in the body of the binding expression. We assume that the content dictionary
foo that defines the bar symbol also supplies a symbol
foo_condition to use for the restriction and translate the example above
to:
<bind>
<csymbol cd="foo">bar</csymbol>
<bvar><ci>x</ci></bvar>
<apply>
<csymbol cd="foo">fooCondition</csymbol>
<apply><ci>P</ci><ci>x</ci></apply>
<apply><sin/><ci>x</ci></apply>
</apply>
</bind>In the case where the binding operator is an identifier given by a ci
element, the treatment is analogous only that we use the general condition symbol instead of a CD-defined one.
4.3.9 Lifted Associative Commutative Operators
Pragmatic Content MathML allows to use a associative operators to be "lifted" to "big operators", for instance the n-ary minimum operator to the minimum operator over sets, as the minimum of squares in this expression:
<apply>
<min/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/><ci>x</ci><interval><cn>-4</cn><cn>4</cn></interval></apply>
</condition>
<apply><power/><ci>x</ci><cn>2</cn></apply>
</apply> While the relation between the nary and the set-based operators is deterministic,
i.e. the induced big operators are fully determined by them, the concepts are quite
different in nature (different notational conventions, different types, different
occurrence schemata). Therefore the MathML 3 content dictionaries provide explicit
symbols for the "big operators", much like MathML2 did with sum
as the big operator for for the n-ary plus symbol, and prod for
times. Concretely, these are big_union,
big_intersect, big_max,
big_min, big_gcd,
big_lcm, big_or,
big_and, big_xor.
| Editorial note: MiKo | |
actually, there are more,
e.g. cartesianproduct; make a complete list
|
|
With these, we can express all pragmatic Content MathML expressions. For instance, the minimum above can be represented in strict Content MathML as
<apply>
<csymbol cd="set1">suchthat</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>S</ci></bvar>
<condition>
<apply><csymbol cd="set1">in</csymbol><ci>S</ci><ci>F</ci></apply>
</condition>
<apply><csymbol cd="set1">setdiff</csymbol><ci>U</ci><ci>S</ci></apply>
</bind>
</apply>For the exact meaning of the new symbols, consult the content dictionaries.
4.3.10 basic elements
4.3.10.1 Interval (interval)
The interval element is used to represent simple mathematical intervals of the
real number line. It takes an optional attribute closure, with a default value
of "closed". Depending on its presence and value, the interval
element corresponds to one of five symbols from the interval1 content
dictionary. If this has the value "open" then interval corresponds
to the interval_oo. With the value
"closed" interval corresponds to the symbol interval_cc, with value "open-closed" to interval_oc, and with "closed-open" to interval_co. The interval1 CD also provides the
symbol interval which cannot be represented in
pragmatic content MathML, since the "closed" is the default value of the
closure attribute.
Content MathML
<interval closure="open">
<ci>x</ci>
<cn>1</cn>
</interval>Default Rendering: Presentation MathML
<mfenced open="(" close=")">
<mi>x</mi><mn>1</mn>
</mfenced>Default Rendering: Image
Content MathML
<interval closure="closed">
<cn>0</cn>
<cn>1</cn>
</interval>Default Rendering: Presentation MathML
<mfenced open="[" close="]"> <mn>0</mn><mn>1</mn> </mfenced>
Default Rendering: Image
Content MathML
<interval closure="open-closed">
<cn>0</cn>
<cn>1</cn>
</interval>Default Rendering: Presentation MathML
<mfenced open="(" close="]">
<mn>0</mn><mn>1</mn>
</mfenced>Default Rendering: Image
Content MathML
<interval closure="closed-open">
<cn>0</cn>
<cn>1</cn>
</interval>Default Rendering: Presentation MathML
<mfenced open="[" close=")"> <mn>0</mn><mn>1</mn> </mfenced>
Default Rendering: Image
The interval element can be used as a container element in pragmatic
Content MathML.
If the optional type attribute of the interval element has the
value "integers", then it corresponds to the symbol integer_interval
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
Finally pragmatic content MathML allows the interval element to be used with a
bvar element and condition defining the interval. Then we
translate this to a set construction:
<interval>
<bvar><ci>x</ci></bvar>
<condition>
<apply><lt/><cn>0</cn><ci>x</ci></apply>
</condition>
</interval>Strict MathML equivlalent
<apply><csymbol cd="set1">suchthat</csymbol>
<csymbol cd="setname1">R</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">lt</csymbol><cn>0</cn><ci>x</ci></apply>
</bind>
</apply>4.3.10.2 Inverse (inverse)
The inverse element is applied to a function in order to construct a generic
expression for the functional inverse of that function. (See also the discussion of
inverse in ???). As with other MathML
functions, inverse may either be applied to arguments, or it may appear alone, in
which case it represents an abstract inversion operator acting on other functions.
A typical use of the inverse element is in an HTML document discussing a
number of alternative definitions for a particular function so that there is a need to
write and define f(-1)(x). To associate a particular definition with
f(-1), use the definitionURL and encoding
attributes.
<apply> <inverse/> <ci> f </ci> </apply>
<apply> <inverse definitionURL="../MyDefinition.htm" encoding="text"/> <ci> f </ci> </apply>
<apply>
<apply><inverse/>
<ci type="matrix"> a </ci>
</apply>
<ci> A </ci>
</apply>The default rendering for a functional inverse makes use of a parenthesized exponent as in f(-1)(x).
4.3.10.3 Lambda (lambda)
The lambda element is used to construct a user-defined function from an
expression, bound variables, and qualifiers. In a lambda construct with n
(possibly 0) bound variables, the first n children are bvar elements
that identify the variables that are used as placeholders in the last child for actual
parameter values. The bound variables can be restricted by an optional
domainofapplication qualifier or one of its shorthand notations. The meaning of
the lambda construct is an n-ary function that returns the expression
in the last child where the bound variables are replaced with the respective
arguments. See ??? for further details.
The domainofapplication child restricts the possible
values of the arguments of the constructed function. For instance, the
following two lambda constructs are representations of a function on
the integers.
<lambda> <bvar><ci> x </ci></bvar> <domainofapplication><integers/></domainofapplication> <apply><sin/><ci> x </ci></apply> </lambda>
If a lambda construct does not contain bound variables, then the
arity of the constructed function is unchanged, and the lambda
construct is redundant, unless it also contains a
domainofapplication construct that restricts existing functional
arguments, as in this example, which is a variant representation for the
function above.
<lambda> <domainofapplication><integers/></domainofapplication> <sin/> </lambda>
In particular, if the last child of a lambda construct is not a
function, say a number, then the lambda construct will not be a
function, but the same number. Of course, in this case a
domainofapplication does not make sense
Content MathML
<lambda>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<sin/>
<ci>x</ci>
</apply>
</lambda>Default Rendering: Presentation MathML
<mrow> <mi>λ</mi><mi>x</mi><mo>.</mo><mfenced><mrow> <mi>sin</mi><mi>x</mi> </mrow></mfenced> </mrow>
Default Rendering: Image
Content MathML
<bind>
<lambda/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<sin/>
<apply>
<plus/>
<ci>x</ci>
<cn>1</cn>
</apply>
</apply>
</bind>Default Rendering: Presentation MathML
<mrow> <mrow> <mi>λ</mi><mrow/><mo>.</mo><mfenced/> </mrow><mo>.</mo><mrow> <mi>sin</mi><mrow> <mo>(</mo><mi>x</mi><mo>+</mo><mn>1</mn><mo>)</mo> </mrow> </mrow> </mrow>
Default Rendering: Image
4.3.10.4 Function composition (compose)
| Editorial note: MiKo | |
| We need to talk about this. | |
The compose element represents the function
composition operator. Note that MathML makes no assumption about the domain
and codomain of the constituent functions in a composition; the domain of the
resulting composition may be empty.
To override the default semantics for the compose element, or to associate a more specific
definition for function composition, use the definitionURL and encoding attributes.
The compose element is an n-ary operator
(see ???).
As an n-ary operator, its operands may also be generated as described in
Section 4.3.9 Lifted Associative Commutative Operators Therefore it may take qualifiers.
<apply> <compose/> <fn><ci> f </ci></fn> <fn><ci> g </ci></fn> </apply>
<apply> <compose/> <ci type="function"> f </ci> <ci type="function"> g </ci> <ci type="function"> h </ci> </apply>
<apply>
<apply><compose/>
<fn><ci> f </ci></fn>
<fn><ci> g </ci></fn>
</apply>
<ci> x </ci>
</apply>
<apply>
<fn><ci> f </ci></fn>
<apply>
<fn><ci> g </ci></fn>
<ci> x </ci>
</apply>
</apply>
4.3.10.5 Identity function (ident)
This is the identity function on a set.
Content MathML
<apply>
<eq/>
<apply>
<compose/>
<ci type="function">f</ci>
<apply>
<inverse/>
<ci type="function">f</ci>
</apply>
</apply>
<ident/>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mi>f</mi><mo>∘</mo><msup> <mi>f</mi><mrow> <mo>(</mo><mn>-1</mn><mo>)</mo> </mrow> </msup> </mrow><mo>=</mo><mo>id</mo> </mrow>
Default Rendering: Image
4.3.10.6 Domain (domain)
This is the domain of a function. It is a unary operation.
Content MathML
<apply>
<eq/>
<apply>
<domain/>
<ci>f</ci>
</apply>
<reals/>
</apply>Default Rendering: Presentation MathML
<mrow>
<mrow>
<mo>domain</mo><mo/><mfenced open="(" close=")" separators=","><mi>f</mi></mfenced>
</mrow><mo>=</mo><mi mathvariant="double-struck">R</mi>
</mrow>Default Rendering: Image
4.3.10.7 codomain (codomain)
This is the codomain, or range, of a function. It is a unary function.
This symbol denotes the range of a function, that is a set that the function will map to. The single argument should be the function whos range is being queried. It should be noted that this is not necessarily equal to the image, it is merely required to contain the image.
Content MathML
<apply>
<eq/>
<apply>
<codomain/>
<ci>f</ci>
</apply>
<rationals/>
</apply>Default Rendering: Presentation MathML
<mrow>
<mrow>
<mo>codomain</mo><mo/><mfenced open="(" close=")" separators=","><mi>f</mi></mfenced>
</mrow><mo>=</mo><mi mathvariant="double-struck">Q</mi>
</mrow>Default Rendering: Image
4.3.10.8 Image (image)
This is the image of a function. It is a unary operator.
The image element denotes the image of a given function, which is the set
of values taken by the function. Every point in the image is generated by the function
applied to some point of the domain.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.10.9 Piecewise declaration (piecewise, piece, otherwise)
The piecewise, piece, and otherwise elements are used to
support "piecewise" declarations of the form "
H(x) = 0 if x less than 0, H(x) = 1
otherwise".
The declaration is constructed using the piecewise element. This contains
zero or more piece elements, and optionally one otherwise element. Each
piece element contains exactly two children. The first child defines the value
taken by the piecewise expression when the condition specified in the associated
second child of the piece is true. The degenerate case of no piece
elements and no otherwise element is treated as undefined for all values of the
domain.
otherwise allows the specification of a value to be taken by the
piecewise function when none of the conditions (second child elements of the
piece elements) is true, i.e. a default value.
It should be noted that no "order of execution" is implied by the
ordering of the piece child elements within piecewise. It is the
responsibility of the author to ensure that the subsets of the function domain defined by
the second children of the piece elements are disjoint, or that, where they
overlap, the values of the corresponding first children of the piece elements
coincide. If this is not the case, the meaning of the expression is undefined.
Content MathML
<piecewise>
<piece>
<apply>
<minus/>
<ci>x</ci>
</apply>
<apply>
<lt/>
<ci>x</ci>
<cn>0</cn>
</apply>
</piece>
<piece>
<cn>0</cn>
<apply>
<eq/>
<ci>x</ci>
<cn>0</cn>
</apply>
</piece>
<piece>
<ci>x</ci>
<apply>
<gt/>
<ci>x</ci>
<cn>0</cn>
</apply>
</piece>
</piecewise>Default Rendering: Presentation MathML
<mrow>
<mo>{</mo><mtable>
<mtr>
<mtd><mrow>
<mo>−</mo><mi>x</mi>
</mrow></mtd><mtd columnalign="left"><mtext>  if  </mtext></mtd><mtd><mrow>
<mi>x</mi><mo><<!--LESS-THAN SIGN--></mo><mn>0</mn>
</mrow></mtd>
</mtr><mtr>
<mtd><mn>0</mn></mtd><mtd columnalign="left"><mtext>  if  </mtext></mtd><mtd><mrow>
<mi>x</mi><mo>=</mo><mn>0</mn>
</mrow></mtd>
</mtr><mtr>
<mtd><mi>x</mi></mtd><mtd columnalign="left"><mtext>  if  </mtext></mtd><mtd><mrow>
<mi>x</mi><mo>><!--GREATER-THAN SIGN--></mo><mn>0</mn>
</mrow></mtd>
</mtr>
</mtable>
</mrow>Default Rendering: Image
4.3.11 Arithmetic, Algebra and Logic
4.3.11.1 Quotient (quotient)
The symbol to represent the integer (binary) division operator. That is, for integers a and b, quotient(a,b) denotes q such that a=b*q+r, with |r| less than |b| and a*r positive.
The quotient element is the operator used for division modulo a
particular base. When the quotient operator is applied to integer arguments
a and b, the result is the "quotient of a
divided by b
". That is, quotient returns the unique
integer q such that a = q
b +
r. (In common usage, q is called the quotient and r
is the remainder.)
Content MathML
<apply>
<quotient/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>⌊</mo><mi>a</mi><mo>/</mo><mi>b</mi><mo>⌋</mo> </mrow>
Default Rendering: Image
4.3.11.2 Factorial (factorial)
The symbol to represent a unary factorial function on non-negative integers.
Factorials are defined by n! = n*(n-1)* ... * 1
Content MathML
<apply>
<factorial/>
<ci>n</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>n</mi><mo>!</mo> </mrow>
Default Rendering: Image
4.3.11.3 Division (divide)
This symbol represents a (binary) division function denoting the first argument right-divided by the second, i.e. divide(a,b)=a*inverse(b). It is the inverse of the multiplication function defined by the symbol times in this CD.
Content MathML
<apply>
<divide/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>/</mo><mi>b</mi> </mrow>
Default Rendering: Image
4.3.11.4 Maximum (max)
This symbol denotes the unary maximum function which takes a set as its argument and returns the maximum element in that set.
Content MathML
<apply>
<max/>
<cn>2</cn>
<cn>3</cn>
<cn>5</cn>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>max</mo><mrow>
<mo>{</mo><mn>2</mn><mo>,</mo><mn>3</mn><mo>,</mo><mn>5</mn><mo>}</mo>
</mrow>
</mrow>Default Rendering: Image
The max operator element can be used as a binding operator in pragmatic
Content MathML. This role is taken over by the big_max symbol in strict
Content MathML. We translate:
<apply>
<max/>
<bvar><ci>x</ci></bvar>
<apply><power/><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_max</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci></apply>
</bind>
</apply>Content MathML
<apply>
<max/>
<bvar>
<ci>y</ci>
</bvar>
<condition>
<apply>
<in/>
<ci>y</ci>
<interval>
<cn>0</cn>
<cn>1</cn>
</interval>
</apply>
</condition>
<apply>
<power/>
<ci>y</ci>
<cn>3</cn>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>max</mo><mrow>
<mo>{</mo><mi>y</mi><mo>|</mo><mrow>
<mi>y</mi><mo>∈</mo><mfenced open="[" close="]">
<mn>0</mn><mn>1</mn>
</mfenced>
</mrow><mo>}</mo>
</mrow>
</mrow>Default Rendering: Image
Content MathML
<apply>
<max/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>max</mo><mrow>
<mo>{</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>}</mo>
</mrow>
</mrow>Default Rendering: Image
4.3.11.5 Minimum (min)
This symbol denotes the unary minimum function which takes a set as its argument and returns the minimum element in that set.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
The min operator element can be used as a binding operator in pragmatic
Content MathML. This role is taken over by the big_min
symbol in strict Content MathML. We translate:
<apply>
<min/>
<bvar><ci>x</ci></bvar>
<apply><power/><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_min</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci></apply>
</bind>
</apply>Content MathML
<apply>
<min/>
<bvar>
<ci>y</ci>
</bvar>
<condition>
<apply>
<in/>
<ci>y</ci>
<interval>
<cn>0</cn>
<cn>1</cn>
</interval>
</apply>
</condition>
<apply>
<power/>
<ci>y</ci>
<cn>2</cn>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>min</mo><mrow>
<mo>{</mo><mi>y</mi><mo>|</mo><mrow>
<mi>y</mi><mo>∈</mo><mfenced open="[" close="]">
<mn>0</mn><mn>1</mn>
</mfenced>
</mrow><mo>}</mo>
</mrow>
</mrow>Default Rendering: Image
Content MathML
<apply>
<min/>
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<notin/>
<ci>x</ci>
<ci type="set"> B</ci>
</apply>
</condition>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>min</mo><mrow>
<mo>{</mo><mi>x</mi><mo>|</mo><mrow>
<mi>x</mi><mo>∉</mo><mi> B</mi>
</mrow><mo>}</mo>
</mrow>
</mrow>Default Rendering: Image
4.3.11.6 Subtraction (minus)
The minus element can be used as a unary arithmetic operator
(e.g. to represent - x), or as a binary arithmetic operator
(e.g. to represent x- y).
If it is used with one argument, minus corresponds to the unary_minus symbol
Content MathML
<apply>
<minus/>
<cn>3</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>−</mo><mn>3</mn> </mrow>
Default Rendering: Image
If it is used with two arguments, minus corresponds to the minus symbol
Content MathML
<apply>
<minus/>
<ci>x</ci>
<ci>y</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>x</mi><mo>−</mo><mi>y</mi> </mrow>
Default Rendering: Image
4.3.11.7 Addition (plus)
The symbol representing an n-ary commutative function plus. If no operands are provided, the expression represents the additive identity. If one operand, a, is provided the expression evaluates to "a". If two or more operands are provided, the expression represents the (semi) group element corresponding to a left associative binary pairing of the operands. The meaning of mixed operand types not covered by the signatures shown here are left up to the target system.
Content MathML
<apply>
<plus/>
<ci>x</ci>
<ci>y</ci>
<ci>z</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>x</mi><mo>+</mo><mi>y</mi><mo>+</mo><mi>z</mi> </mrow>
Default Rendering: Image
The lcm symbol can be used as a binding operator in pragmatic Content
MathML. This role is taken over by the big_lcm symbol in strict Content
MathML.
<apply>
<lcm/>
<bvar><ci>x</ci></bvar>
<ci>x</ci>
</apply>Strict MathML equivlalent
<apply>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<ci>x</ci>
</bind>
</apply>4.3.11.8 Exponentiation (power)
This symbol represents a power function. The first argument is raised to the power of the second argument. When the second argument is not an integer, powering is defined in terms of exponentials and logarithms for the complex and real numbers. This operator can represent general powering.
Content MathML
<apply>
<power/>
<ci>x</ci>
<cn>3</cn>
</apply>Default Rendering: Presentation MathML
<msup> <mi>x</mi><mn>3</mn> </msup>
Default Rendering: Image
4.3.11.9 Remainder (rem)
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.11.10 Multiplication (times)
The symbol representing an n-ary multiplication function.
Content MathML
<apply>
<times/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo/><mi>b</mi> </mrow>
Default Rendering: Image
4.3.11.11 Root (root)
The kind of root to be taken is specified by a "degree" child, which
should be given as the second child of the apply element enclosing the
root element. Thus, square roots correspond to the case where
degree contains the value 2, cube roots correspond to 3, and so on.
Note that pragmatic MathML supports a degree element in the container
representation. If no degree is present, a default value of 2 is used.
Content MathML
<apply>
<root/>
<degree>
<ci>n</ci>
</degree>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mroot> <mi>a</mi><mi>n</mi> </mroot>
Default Rendering: Image
4.3.11.12 Greatest common divisor (gcd)
This is the n-ary operator used to construct an expression which represents the greatest common divisor of its arguments. If no argument is provided, the gcd is 0. If one argument is provided, the gcd is that argument.
Content MathML
<apply>
<gcd/>
<ci>a</ci>
<ci>b</ci>
<ci>c</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>gcd</mo><mo/><mfenced open="(" close=")" separators=",">
<mi>a</mi><mi>b</mi><mi>c</mi>
</mfenced>
</mrow>Default Rendering: Image
This default rendering is English-language locale specific: other locales may have different default renderings.
The gcd symbol can be used as a binding operator in pragmatic Content
MathML. This role is taken over by the big_gcd symbol in strict Content
MathML. We translate:
<apply>
<gcd/>
<bvar><ci>x</ci></bvar>
<ci>x</ci>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_gcd</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<ci>x</ci>
</bind>
</apply>4.3.11.13 And (and)
This symbol represents the logical and function which is an n-ary function taking boolean arguments and returning a boolean value. It is true if all arguments are true or false otherwise.
Content MathML
<apply>
<and/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>∧</mo><mi>b</mi> </mrow>
Default Rendering: Image
The and operator element can be used as a binding operator in pragmatic
Content MathML. This role is taken over by the big_and symbol in strict
Content MathML.
<apply>
<and/>
<bvar><ci>x</ci></bvar>
<apply><eq/><ci>x</ci><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_and</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">eq</csymbol><ci>x</ci><ci>x</ci></apply>
</bind>
</apply>4.3.11.14 Or (or)
This symbol represents the logical or function which is an n-ary function taking boolean arguments and returning a boolean value. It is true if any of the arguments are true or false otherwise.
Content MathML
<apply>
<or/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>∨</mo><mi>b</mi> </mrow>
Default Rendering: Image
The or operator element can be used as a binding operator in pragmatic
Content MathML. This role is taken over by the big_or symbol in strict
Content MathML.
<apply>
<or/>
<bvar><ci>x</ci></bvar>
<apply><eq/><ci>x</ci><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_or</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">eq</csymbol><ci>x</ci><ci>x</ci></apply>
</bind>
</apply>4.3.11.15 Exclusive Or (xor)
This symbol represents the logical xor function which is an n-ary function taking boolean arguments and returning a boolean value. It is true if there are an odd number of true arguments or false otherwise.
Content MathML
<apply>
<xor/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>xor</mo><mi>b</mi> </mrow>
Default Rendering: Image
The xor operator element can be used as a binding operator in pragmatic
Content MathML. This role is taken over by the big_xor symbol in strict
Content MathML.
<apply>
<xor/>
<bvar><ci>x</ci></bvar>
<apply><eq/><ci>x</ci><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_xor</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">eq</csymbol><ci>x</ci><ci>x</ci></apply>
</bind>
</apply>4.3.11.16 Not (not)
This symbol represents the logical not function which takes one boolean argument, and returns the opposite boolean value.
Content MathML
<apply>
<not/>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>¬</mo><mi>a</mi> </mrow>
Default Rendering: Image
4.3.11.17 Implies (implies)
This symbol represents the logical implies function which takes two boolean expressions as arguments. It evaluates to false if the first argument is true and the second argument is false, otherwise it evaluates to true.
Content MathML
<apply>
<implies/>
<ci>A</ci>
<ci>B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>⇒</mo><mi>B</mi> </mrow>
Default Rendering: Image
4.3.11.18 Universal quantifier (forall)
This symbol represents the universal ("for all") quantifier which takes two arguments. It is usually used in conjunction with one or more bound variables and an assertion.
Content MathML
<bind>
<forall/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<eq/>
<apply>
<minus/>
<ci>x</ci>
<ci>x</ci>
</apply>
<cn>0</cn>
</apply>
</bind>Default Rendering: Presentation MathML
<mrow> <mi>forall</mi><mo>.</mo><mrow> <mrow> <mi>x</mi><mo>−</mo><mi>x</mi> </mrow><mo>=</mo><mn>0</mn> </mrow> </mrow>
Default Rendering: Image
When the forall element is used with a condition qualifier the
strict equivalent is constructed with the help of logical implication.
Content MathML
<bind>
<forall/>
<bvar>
<ci>p</ci>
</bvar>
<bvar>
<ci>q</ci>
</bvar>
<condition>
<apply>
<and/>
<apply>
<in/>
<ci>p</ci>
<rationals/>
</apply>
<apply>
<in/>
<ci>q</ci>
<rationals/>
</apply>
<apply>
<lt/>
<ci>p</ci>
<ci>q</ci>
</apply>
</apply>
</condition>
<apply>
<lt/>
<ci>p</ci>
<apply>
<power/>
<ci>q</ci>
<cn>2</cn>
</apply>
</apply>
</bind>Default Rendering: Presentation MathML
<mrow> <mi>forall</mi><mo>.</mo><mrow> <mrow> <mi>p</mi><mo>∈</mo><mi mathvariant="double-struck">Q</mi> </mrow><mo>∧</mo><mrow> <mi>q</mi><mo>∈</mo><mi mathvariant="double-struck">Q</mi> </mrow><mo>∧</mo><mrow> <mo>(</mo><mi>p</mi><mo><<!--LESS-THAN SIGN--></mo><mi>q</mi><mo>)</mo> </mrow> </mrow><mrow> <mi>p</mi><mo><<!--LESS-THAN SIGN--></mo><msup> <mi>q</mi><mn>2</mn> </msup> </mrow> </mrow>
Default Rendering: Image
The universal quantifier can also be used with the domainofapplication
qualifier to restrict the range of the bound variable. In this case, we use the
every symbol from the quant2 content
dictionary.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
Note:
The second and third examples in this section are correct MathML expressions of False mathematical statements.
4.3.11.19 Existential quantifier (exists)
This symbol represents the existential ("there exists") quantifier which takes two arguments. It is used in conjunction with one or more bound variables and an assertion.
Content MathML
<bind>
<exists/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<eq/>
<apply>
<ci>f</ci>
<ci>x</ci>
</apply>
<cn>0</cn>
</apply>
</bind>Default Rendering: Presentation MathML
<mrow>
<mi>exists</mi><mo>.</mo><mrow>
<mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=","><mi>x</mi></mfenced>
</mrow><mo>=</mo><mn>0</mn>
</mrow>
</mrow>Default Rendering: Image
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
When the exists element is used with a condition qualifier the
strict equivalent is constructed with the help of logical conjunction.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
The existential quantifier can also be used with the domainofapplication
qualifier to restrict the range of the bound variable. In this case, we use the
some symbol from the quant2 content
dictionary.
4.3.11.20 Absolute Value (abs)
A unary operator which represents the absolute value of its argument. The argument should be numerically valued. In the complex case this is often referred to as the modulus.
Content MathML
<apply>
<abs/>
<ci>x</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>|</mo><mi>x</mi><mo>|</mo> </mrow>
Default Rendering: Image
4.3.11.21 Complex conjugate (conjugate)
The unary "conjugate" arithmetic operator is used to represent the complex conjugate of its argument.
Content MathML
<apply>
<conjugate/>
<apply>
<plus/>
<ci>x</ci>
<apply>
<times/>
<cn>␘</cn>
<ci>y</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mover> <mrow> <mi>x</mi><mo>+</mo><mrow> <mn>␘</mn><mo/><mi>y</mi> </mrow> </mrow><mo>¯</mo> </mover>
Default Rendering: Image
4.3.11.22 Argument (arg)
This symbol represents the unary function which returns the argument of a complex number, viz. the angle which a straight line drawn from the number to zero makes with the Real line (measured anti-clockwise). The argument to the symbol is the complex number whos argument is being taken.
Content MathML
<apply>
<arg/>
<apply>
<plus/>
<ci> x </ci>
<apply>
<times/>
<imaginaryi/>
<ci>y</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>arg</mo><mo/><mfenced open="(" close=")" separators=","><mrow>
<mi> x </mi><mo>+</mo><mrow>
<mi>i</mi><mo/><mi>y</mi>
</mrow>
</mrow></mfenced>
</mrow>Default Rendering: Image
4.3.11.23 Real part (real)
This symbol is a unary operator used to construct an expression representing the "real" part of a complex number, that is the x component in x + iy.
Content MathML
<apply>
<real/>
<apply>
<plus/>
<ci>x</ci>
<apply>
<times/>
<imaginaryi/>
<ci>y</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>ℛ</mo><mo/><mfenced open="(" close=")" separators=","><mrow>
<mi>x</mi><mo>+</mo><mrow>
<mi>i</mi><mo/><mi>y</mi>
</mrow>
</mrow></mfenced>
</mrow>Default Rendering: Image
4.3.11.24 Imaginary part (imaginary)
This symbol represents unary function used to construct the imaginary part of a complex number, i.e. the y component in x+iy.
Content MathML
<apply>
<imaginary/>
<apply>
<plus/>
<ci>x</ci>
<apply>
<times/>
<imaginaryi/>
<ci>y</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>ℑ</mo><mo/><mfenced open="(" close=")" separators=","><mrow>
<mi>x</mi><mo>+</mo><mrow>
<mi>i</mi><mo/><mi>y</mi>
</mrow>
</mrow></mfenced>
</mrow>Default Rendering: Image
4.3.11.25 Lowest common multiple (lcm)
This n-ary operator is used to construct an expression which represents the least common multiple of its arguments. If no argument is provided, the lcm is 1. If one argument is provided, the lcm is that argument. The least common multiple of x and 1 is x.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
This default rendering is English-language locale specific: other locales may have different default renderings.
The lcm symbol can be used as a binding operator in pragmatic Content
MathML. This role is taken over by the big_lcm symbol in strict Content
MathML. We translate:
<apply>
<lcm/>
<bvar><ci>x</ci></bvar>
<ci>x</ci>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">big_lcm</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<ci>x</ci>
</bind>
</apply>4.3.11.26 Floor (floor)
The round down (towards negative infinity) operation. This function takes one real number as an argument and retunrns an integer.
Content MathML
<apply>
<floor/>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>⌊</mo><mi>a</mi><mo>⌋</mo> </mrow>
Default Rendering: Image
4.3.11.27 Ceiling (ceiling)
The ceiling function is used to round-up (towards positive infinity). This function takes one real number as an argument and retunrns an integer.
Content MathML
<apply>
<ceiling/>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>⌈</mo><mi>a</mi><mo>⌉</mo> </mrow>
Default Rendering: Image
4.3.12 Relations
4.3.12.1 Equals (eq)
This symbol represents the binary equality function.
Content MathML
<apply>
<eq/>
<cn type="rational">2<sep/>4</cn>
<cn type="rational">1<sep/>2</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mn>2</mn><mo>/</mo><mn>4</mn> </mrow><mo>=</mo><mrow> <mn>1</mn><mo>/</mo><mn>2</mn> </mrow> </mrow>
Default Rendering: Image
In pragmatic content MathML, the eq element can be used as an n-ary
operator. We interpret the n-ary application as a conjunction of binary ones and translate:
<apply><eq/><ci>x</ci><ci>y</ci><ci>z</ci><ci>w</ci></apply>
Strict MathML equivlalent
<apply> <csymbol cd="logic1">and</csymbol> <apply><csymbol cd="relation1">eq</csymbol><ci>x</ci><ci id="arg_eq_2">y</ci></apply> <apply><csymbol cd="relation1">eq</csymbol><share href="#arg_eq_2"/><ci id="arg_eq_3">z</ci></apply> <apply><csymbol cd="relation1">eq</csymbol><share href="#arg_eq_3"/><ci>w</ci></apply> </apply>
| Editorial note: MiKo | |
| maybe we should deprecate the following usage? | |
In pragmatic content MathML, the eq element can be used as a binding operator
taking qualifiers. For strict content MathML we
translate this using a universally quantified expression:
<apply><eq/> <bvar><ci>i</ci></bvar> <condition><ci>C</ci></condition> <apply><ci>Ai</ci></apply> </apply>
Strict MathML equivlalent
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>i</ci></bvar>
<bvar><ci>j</ci></bvar>
<apply>
<csymbol cd="logic1">implies</csymbol>
<ci>C</ci>
<apply><csymbol cd="relation1">eq</csymbol><ci>Ai</ci><ci>Aj</ci></apply>
</apply>
</bind>4.3.12.2 Not Equals (neq)
This symbol represents the binary inequality relation, i.e. the relation "not equal to" which returns true unless the two arguments are equal.
Content MathML
<apply>
<neq/>
<cn>3</cn>
<cn>4</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mn>3</mn><mo>≠</mo><mn>4</mn> </mrow>
Default Rendering: Image
4.3.12.3 Greater than (gt)
This symbol represents the binary greater than function which returns true if the first argument is greater than the second, it returns false otherwise.
Content MathML
<apply>
<gt/>
<cn>3</cn>
<cn>2</cn>
</apply>Default Rendering: Presentation MathML
<mrow>
<mn>3</mn><mo>><!--GREATER-THAN SIGN--></mo><mn>2</mn>
</mrow>Default Rendering: Image
In pragmatic content MathML, the gt element can be used as an
n-ary operator. We interpret the n-ary application as a
conjunction of binary ones and translate:
<apply><gt/><ci>x</ci><ci>y</ci><ci>z</ci><ci>w</ci></apply>
Strict MathML equivlalent
<apply> <csymbol cd="logic1">and</csymbol> <apply><csymbol cd="relation1">gt</csymbol><ci>x</ci><ci id="arg_gt_2">y</ci></apply> <apply><csymbol cd="relation1">gt</csymbol><share href="#arg_gt_2"/><ci id="arg_gt_3">z</ci></apply> <apply><csymbol cd="relation1">gt</csymbol><share href="#arg_gt_3"/><ci>w</ci></apply> </apply>
| Editorial note: MiKo | |
| maybe we should deprecate the following usage? | |
In pragmatic content MathML, the gt element can also be used as a binding
operator taking qualifiers. For strict content
MathML we translate this using a universally quantified expression:
<apply><gt/>
<bvar><ci>i</ci></bvar>
<domainofapplication><ci>C</ci></domainofapplication>
<apply><ci>Ai</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>i</ci></bvar>
<apply>
<csymbol cd="quant1">implies</csymbol>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>j</ci></bvar>
<apply>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<apply>
<csymbol cd="logic1">implies</csymbol>
<apply><csymbol cd="relation1">lt</csymbol><ci>i</ci><ci>j</ci></apply>
<apply><csymbol cd="relation1">gt</csymbol><ci>Ai</ci><ci>Aj</ci></apply>
</apply>
</apply>
</bind>
</apply>
</bind>Note that this only makes sense, if the domain C of application is ordered,
we have used the ordering relation lt on C. Furthermore, we have used
the fact that gt is transitive.
4.3.12.4 Less Than (lt)
This symbol represents the binary less than function which returns true if the first argument is less than the second, it returns false otherwise.
Content MathML
<apply>
<lt/>
<cn>2</cn>
<cn>3</cn>
<cn>4</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mn>2</mn><mo><<!--LESS-THAN SIGN--></mo><mn>3</mn><mo><<!--LESS-THAN SIGN--></mo><mn>4</mn> </mrow>
Default Rendering: Image
In pragmatic content MathML, the lt element can be used as an n-ary
operator. We interpret the n-ary application as a conjunction of binary ones and translate:
<apply><lt/><ci>x</ci><ci>y</ci><ci>z</ci><ci>w</ci></apply>
Strict MathML equivlalent
<apply> <csymbol cd="logic1">and</csymbol> <apply><csymbol cd="relation1">lt</csymbol><ci>x</ci><ci id="arg_lt_2">y</ci></apply> <apply><csymbol cd="relation1">lt</csymbol><share href="#arg_lt_2"/><ci id="arg_lt_3">z</ci></apply> <apply><csymbol cd="relation1">lt</csymbol><share href="#arg_lt_3"/><ci>w</ci></apply> </apply>
| Editorial note: MiKo | |
| maybe we should deprecate the following usage? | |
In pragmatic content MathML, the lt element can also be used as a binding
operator taking qualifiers. For strict content
MathML we translate this using a universally quantified expression:
<apply><lt/>
<bvar><ci>i</ci></bvar>
<domainofapplication><ci>C</ci></domainofapplication>
<apply><ci>Ai</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>i</ci></bvar>
<apply>
<csymbol cd="quant1">implies</csymbol>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>j</ci></bvar>
<apply>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<apply>
<csymbol cd="logic1">implies</csymbol>
<apply><csymbol cd="relation1">lt</csymbol><ci>i</ci><ci>j</ci></apply>
<apply><csymbol cd="relation1">lt</csymbol><ci>Ai</ci><ci>Aj</ci></apply>
</apply>
</apply>
</bind>
</apply>
</bind>Note that this only makes sense, if the domain C of application is ordered,
we have used the ordering relation lt on C. Furthermore, we have used
the fact that lt is transitive.
4.3.12.5 Greater Than or Equal (geq)
This symbol represents the binary greater than or equal to function which returns true if the first argument is greater than or equal to the second, it returns false otherwise.
Content MathML
<apply>
<geq/>
<cn>4</cn>
<cn>3</cn>
<cn>3</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mn>4</mn><mo>≥</mo><mn>3</mn><mo>≥</mo><mn>3</mn> </mrow>
Default Rendering: Image
In pragmatic content MathML, the geq element can be used as an n-ary
operator. We interpret the n-ary application as a conjunction of binary ones and translate:
<apply><geq/><ci>x</ci><ci>y</ci><ci>z</ci><ci>w</ci></apply>
Strict MathML equivlalent
<apply> <csymbol cd="logic1">and</csymbol> <apply><csymbol cd="relation1">geq</csymbol><ci>x</ci><ci id="arg_geq_2">y</ci></apply> <apply><csymbol cd="relation1">geq</csymbol><share href="#arg_geq_2"/><ci id="arg_geq_3">z</ci></apply> <apply><csymbol cd="relation1">geq</csymbol><share href="#arg_geq_3"/><ci>w</ci></apply> </apply>
| Editorial note: MiKo | |
| maybe we should deprecate the following usage? | |
In pragmatic content MathML, the geq element can also be used as a binding
operator taking qualifiers. For strict content
MathML we translate this using a universally quantified expression:
<apply><geq/>
<bvar><ci>i</ci></bvar>
<domainofapplication><ci>C</ci></domainofapplication>
<apply><ci>Ai</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>i</ci></bvar>
<apply>
<csymbol cd="quant1">implies</csymbol>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>j</ci></bvar>
<apply>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<apply>
<csymbol cd="logic1">implies</csymbol>
<apply><csymbol cd="relation1">lt</csymbol><ci>i</ci><ci>j</ci></apply>
<apply><csymbol cd="relation1">geq</csymbol><ci>Ai</ci><ci>Aj</ci></apply>
</apply>
</apply>
</bind>
</apply>
</bind>Note that this only makes sense, if the domain C of application is ordered,
we have used the ordering relation lt on C. Furthermore, we have used
the fact that geq is transitive.
4.3.12.6 Less Than or Equal (leq)
This symbol represents the binary less than or equal to function which returns true if the first argument is less than or equal to the second, it returns false otherwise.
Content MathML
<apply>
<leq/>
<cn>3</cn>
<cn>3</cn>
<cn>4</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mn>3</mn><mo>≤</mo><mn>3</mn><mo>≤</mo><mn>4</mn> </mrow>
Default Rendering: Image
In pragmatic content MathML, the leq element can be used as an n-ary
operator. We interpret the n-ary application as a conjunction of binary ones and translate:
<apply><leq/><ci>x</ci><ci>y</ci><ci>z</ci><ci>w</ci></apply>
Strict MathML equivlalent
<apply> <csymbol cd="logic1">and</csymbol> <apply><csymbol cd="relation1">leq</csymbol><ci>x</ci><ci id="arg_leq_2">y</ci></apply> <apply><csymbol cd="relation1">leq</csymbol><share href="#arg_leq_2"/><ci id="arg_leq_3">z</ci></apply> <apply><csymbol cd="relation1">leq</csymbol><share href="#arg_leq_3"/><ci>w</ci></apply> </apply>
| Editorial note: MiKo | |
| maybe we should deprecate the following usage? | |
In pragmatic content MathML, the leq element can also be used as a binding
operator taking qualifiers. For strict content
MathML we translate this using a universally quantified expression:
<apply><leq/>
<bvar><ci>i</ci></bvar>
<domainofapplication><ci>C</ci></domainofapplication>
<apply><ci>Ai</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>i</ci></bvar>
<apply>
<csymbol cd="quant1">implies</csymbol>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>j</ci></bvar>
<apply>
<apply><csymbol cd="set1">in</csymbol><ci>i</ci><ci>S</ci></apply>
<apply>
<csymbol cd="logic1">implies</csymbol>
<apply><csymbol cd="relation1">geq</csymbol><ci>i</ci><ci>j</ci></apply>
<apply><csymbol cd="relation1">leq</csymbol><ci>Ai</ci><ci>Aj</ci></apply>
</apply>
</apply>
</bind>
</apply>
</bind>Note that this only makes sense, if the domain C of application is ordered,
we have used the ordering relation lt on C. Furthermore, we have used
the fact that leq is transitive.
4.3.12.7 Equivalent (equivalent)
This symbol is used to show that two boolean expressions are logically equivalent, that is have the same boolean value for any inputs.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
In pragmatic content MathML, the equivalent element can be used as an n-ary
operator. We interpret the n-ary application as a conjunction of binary ones and translate:
<apply><equivalent/><ci>x</ci><ci>y</ci><ci>z</ci><ci>w</ci></apply>
Strict MathML equivlalent
<apply> <csymbol cd="logic1">and</csymbol> <apply><csymbol cd="relation1">equivalent</csymbol><ci>x</ci><ci id="arg_eqv_2">y</ci></apply> <apply><csymbol cd="relation1">equivalent</csymbol><share href="#arg_eqv_2"/><ci id="arg_eqv_3">z</ci></apply> <apply><csymbol cd="relation1">equivalent</csymbol><share href="#arg_eqv_3"/><ci>w</ci></apply> </apply>
| Editorial note: MiKo | |
| maybe we should deprecate the following usage? | |
In pragmatic content MathML, the equivalent element can also be used as a binding operator
taking qualifiers. For strict content MathML we
translate this using a universally quantified expression:
<apply><equivalent/> <bvar><ci>i</ci></bvar> <condition><ci>C</ci></condition> <apply><ci>Ai</ci></apply> </apply>
Strict MathML equivlalent
<bind>
<csymbol cd="quant1">forall</csymbol>
<bvar><ci>i</ci></bvar>
<bvar><ci>j</ci></bvar>
<apply>
<csymbol cd="logic1">implies</csymbol>
<ci>C</ci>
<apply><csymbol cd="relation1">equivalent</csymbol><ci>Ai</ci><ci>Aj</ci></apply>
</apply>
</bind>4.3.12.8 Approximately (approx)
This symbol is used to denote the approximate equality of its two arguments.
Content MathML
<apply>
<approx/>
<pi/>
<cn type="rational">22<sep/>7</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>π</mi><mo>≃</mo><mrow> <mn>22</mn><mo>/</mo><mn>7</mn> </mrow> </mrow>
Default Rendering: Image
4.3.12.9 Factor Of (factorof)
This is the binary operator that is used to indicate the mathematical relationship a "is a factor of" b, where a is the first argument and b is the second. This relationship is true if and only if b mod a = 0.
Content MathML
<apply>
<factorof/>
<ci>a</ci>
<ci>b</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>|</mo><mi>b</mi> </mrow>
Default Rendering: Image
4.3.13 Calculus and Vector Calculus
| Editorial note: MiKo | |
| The material in this section needs to be reworked for the new calculus3 CD | |
4.3.13.1 Integral (int)
The int element is the operator element for a definite or indefinite
integral. It can be applied directly to a function or to an expression with a bound
variable.
As an indefinite integral applied to a function the int element corresponds to
the int symbol from the calculus1 content
dictionary.
This symbol is used to represent indefinite integration of unary functions. The argument is the unary function.
Content MathML
<apply><eq/>
<apply><int/><sin/></apply>
<cos/>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <msubsup> <mi>∫</mi><mrow/><mrow/> </msubsup><mi>sin</mi> </mrow><mo>=</mo><mi>cos</mi> </mrow>
Default Rendering: Image
As an definite integral applied to a function the int element corresponds to
the defint symbol from the calculus1
content dictionary.
This symbol is used to represent definite integration of unary functions. It takes two arguments; the first being the range (e.g. a set) of integration, and the second the function.
Content MathML
<apply>
<int/>
<apply><interval/><ci>a</ci><ci>b</ci></apply>
<cos/>
</apply>Default Rendering: Presentation MathML
<mrow> <msubsup> <mi>∫</mi><mrow/><mrow/> </msubsup><mi>cos</mi> </mrow>
Default Rendering: Image
The int element can also be used with bound variables serving as the
integration variables. Here, definite integrals are indicated by providing a qualifier
element specifying a domain of integration.
As a definite integral applied to an expression the int element corresponds to
the defintbounds symbol from the calculus1 content dictionary.
This symbol is used to construct binding operator for definite integration of unary functions. It takes two arguments: the lower and upper bounds of the the range of integration.
This example specifies an interval of the real line as the domain of integration with
an interval element. In this form the integrand is provided as a function and no
mention is made of a bound variable. We translate:
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<apply><interval/><ci>a</ci><ci>b</ci></apply>
<apply><cos/><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<apply>
<csymbol cd="calculus3">defint</csymbol>
<csymbol cd="interval1">interval</csymbol><ci>a</ci><ci>b</ci>
</apply>
<apply><csymbol cd="transc1">cos</csymbol><ci>x</ci></apply>
</bind>The next example specifies the integrand using an expression involving a bound variable
and makes it a definite integral by using the qualifiers lowlimit,
uplimit to place restrictions on the bound variable. We translate
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><ci>a</ci></uplimit>
<apply><ci>f</ci><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<apply><csymbol cd="calculus3">defintbounds</csymbol><cn>0</cn><ci>a</ci></apply>
<bvar><ci>x</ci></bvar>
<apply><ci>f</ci><ci>x</ci></apply>
</bind>The final example specifies the domain of integration with a bound variable and a
condition element We translate.
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/><ci>x</ci><ci type="set">D</ci></apply>
</condition>
<apply><ci type="function">f</ci><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<bind>
<apply>
<csymbol cd="calculus3">defintcond</csymbol>
<apply><csymbol cd="set1">in</csymbol><ci>x</ci><ci type="set">D</ci></apply>
</apply>
<bvar><ci>x</ci></bvar>
<apply><ci type="function">f</ci><ci>x</ci></apply>
</bind>Note that the pragmatic use of the condition element extends to multivariate domains by
using extra bound variables and a domain corresponding to a cartesian product as in
<bind>
<int/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>x</ci></apply>
<apply><leq/><ci>x</ci><cn>1</cn></apply>
<apply><leq/><cn>0</cn><ci>y</ci></apply>
<apply><leq/><ci>y</ci><cn>1</cn></apply>
</apply>
</condition>
<apply><times/>
<apply><power/><ci>x</ci><cn>2</cn></apply>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>
</bind>Strict MathML equivlalent
<bind>
<csymbol cd="calculus1">defint</csymbol>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<apply>
<csymbol cd="set1">suchthat</csymbol>
<apply>
<csymbol cd="set1">cartesianproduct</csymbol>
<csymbol cd="setname1">R</csymbol>
<csymbol cd="setname1">R</csymbol>
</apply>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="arith1">leq</csymbol><cn>0</cn><ci>x</ci></apply>
<apply><csymbol cd="arith1">leq</csymbol><ci>x</ci><cn>1</cn></apply>
<apply><csymbol cd="arith1">leq</csymbol><cn>0</cn><ci>y</ci></apply>
<apply><csymbol cd="arith1">leq</csymbol><ci>y</ci><cn>1</cn></apply>
</apply>
<apply><csymbol cd="arith1">times</csymbol>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><cn>2</cn></apply>
<apply><csymbol cd="arith1">power</csymbol><ci>y</ci><cn>3</cn></apply>
</apply>
</apply>
</bind>4.3.13.2 Differentiation (diff)
The diff element is the differentiation operator element for functions or
expressions of a single variable. It may be applied directly to an actual function
thereby denoting a function which is the derivative of the original function, or it can be
applied to an expression involving a single variable.
When applied to a function, the diff element corresponds to the diff symbol from the calculus1 content
dictionary.
This symbol is used to express ordinary differentiation of a function with a single variable. The only argument is the function.
Content MathML
<apply><eq/>
<apply><diff/><sin/></apply>
<cos/>
</apply>Default Rendering: Presentation MathML
<mrow> <mfrac> <mrow> <mo>d</mo><mi>sin</mi> </mrow><mo>d</mo> </mfrac><mo>=</mo><mi>cos</mi> </mrow>
Default Rendering: Image
Content MathML
<apply><diff/><ci>f</ci></apply>
Default Rendering: Presentation MathML
<msup> <mi>f</mi><mo>′</mo> </msup>
Default Rendering: Image
For the expression case the actual variable is designated by a bvar element
that is a child of the containing apply element. The bvar element may
also contain a degree element, which specifies the order of the derivative to be
taken.
| Editorial note: MiKo | |
| The following text is left over from an earlier discussion, it should probably be rewritten to calculus3 | |
The derivative with respect to x of an expression in x such as f (x) can be written as:
<apply> <diff/> <bvar><ci> x </ci></bvar> <apply><ci>f</ci><ci>x</ci></apply> </apply>
In pragmatic Content MathML the diff operator can be applied to an
expression involving a single variable such as sin(x), or
cos(x). or a polynomial in x. For the expression case the
actual variable is designated by a bvar element that is a child of the
containing apply element. To translate this usage to strict Content
MathML, we add a lambda construction.
<apply>
<diff/>
<bvar><ci>x</ci></bvar>
<apply><sin/><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="calculus1">diff</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>The bvar element may also contain a degree element, which
specifies the order of the derivative to be taken. To achieve this effect in
strict Content MathML, we use the nthdiff symbol.
<apply>
<diff/>
<bvar>
<degree><cn>2</cn></degree>
<ci>x</ci>
</bvar>
<apply><sin/><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="calculus1">nthdiff</csymbol>
<cn>2</cn>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>4.3.13.3 Partial Differentiation (partialdiff)
The partialdiff element is the partial differentiation operator element for
functions or expressions in several variables. It may be applied directly to an actual
function thereby denoting a function which is the derivative of the original function, or
it can be applied to an expression involving a single variable.
| Editorial note: MiKo | |
talk about the type attribute here, which can have the values
"function" or "algebraic".
|
|
For the case of partial differentiation of a function, the containing apply
takes two child elements: firstly a list of indices indicating by position which
coordinates are involved in constructing the partial derivatives, and secondly the actual
function to be partially differentiated. The coordinates may be repeated.
When applied to a function, the diff element corresponds to the partialdiff symbol from the calculus1 content
dictionary.
This symbol is used to express ordinary differentiation of a function with a single variable. The only argument is the function.
Content MathML
<apply>
<partialdiff/>
<bvar>
<ci>x</ci>
<degree>
<ci>m</ci>
</degree>
</bvar>
<bvar>
<ci>y</ci>
<degree>
<ci>n</ci>
</degree>
</bvar>
<degree>
<ci>k</ci>
</degree>
<apply>
<ci type="function">f</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mfrac>
<mrow>
<msup>
<mo>∂</mo><mi>k</mi>
</msup><mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mi>y</mi>
</mfenced>
</mrow>
</mrow><mrow>
<mrow>
<mo>∂</mo><msup>
<mi>x</mi><mi>m</mi>
</msup>
</mrow><mrow>
<mo>∂</mo><msup>
<mi>y</mi><mi>n</mi>
</msup>
</mrow>
</mrow>
</mfrac>Default Rendering: Image
Content MathML
<apply>
<partialdiff/>
<bvar>
<ci>x</ci>
</bvar>
<bvar>
<ci>y</ci>
</bvar>
<apply>
<ci type="function">f</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mfrac>
<mrow>
<msup>
<mo>∂</mo><mn>2</mn>
</msup><mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mi>y</mi>
</mfenced>
</mrow>
</mrow><mrow>
<mrow>
<mo>∂</mo><msup>
<mi>x</mi><mrow/>
</msup>
</mrow><mrow>
<mo>∂</mo><msup>
<mi>y</mi><mrow/>
</msup>
</mrow>
</mrow>
</mfrac>Default Rendering: Image
Content MathML
<apply>
<partialdiff/>
<list>
<cn>1</cn>
<cn>1</cn>
<cn>3</cn>
</list>
<ci type="function">f</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <msub> <mo>D</mo><mrow> <mn>1</mn><mo>,</mo><mn>1</mn><mo>,</mo><mn>3</mn> </mrow> </msub><mi>f</mi> </mrow>
Default Rendering: Image
In the case of algebraic expressions, the bound variables are given by bvar
elements, which are children of the containing apply element. The bvar
elements may also contain degree element, which specify the order of the partial
derivative to be taken in that variable.
For the expression case the actual variable is designated by a bvar element
that is a child of the containing apply element. The bvar elements may
also contain a degree element, which specifies the order of the derivative to be
taken.
Where a total degree of differentiation must be specified, this is indicated by use of
a degree element at the top level, i.e. without any associated bvar, as
a child of the containing apply element.
| Editorial note: MiKo | |
| The following text was left over from the CD | |
In pragmatic Content MathML, the partialdiff operator can be applied to
an expression with bound variables given by bvar elements, which are
children of the containing apply element. The bvar elements may
also contain degree element, which specify the order of the partial
derivative to be taken in that variable. In strict Content MathML, the degrees are
given as a list in the first argument of the partialdiff symbol.
<apply>
<partialdiff/>
<bvar>
<ci>x</ci>
<degree>
<ci>n</ci>
</degree>
</bvar>
<bvar>
<ci>y</ci>
<degree>
<ci>m</ci>
</degree>
</bvar>
<apply>
<sin/>
<apply>
<times/>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="claculus1">partialdiff</csymbol>
<apply>
<csymbol cd="list1">list</csymbol>
<ci>n</ci>
<ci>m</ci>
</apply>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar>
<ci>x</ci>
</bvar>
<bvar>
<ci>y</ci>
</bvar>
<apply>
<csymbol cd="transc1">sin</csymbol>
<apply>
<csymbol cd="arith1">times</csymbol>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>
</bind>
</apply>Where a total degree of differentiation must be specified, this is indicated by
use of a degree element at the top level, i.e. without any associated
bvar, as a child of the containing apply element. Each
degree schema used with partialdiff is expected to contain a
single child schema. For example,
<apply>
<partialdiff/>
<bvar>
<degree>
<cn>2</cn>
</degree>
<ci>x</ci>
</bvar>
<bvar>
<ci>y</ci>
</bvar>
<bvar>
<ci>x</ci>
</bvar>
<degree>
<cn>4</cn>
</degree>
<ci type="function">f</ci>
</apply>
denotes the mixed partial derivative ( d4 / d2 x dy dx ) f. In strict Content MathML, the overall degree cannot be given.
4.3.13.4 Divergence (divergence)
The divergence element is the vector calculus divergence operator, often
called div.
This symbol is used to represent the divergence function. It takes one argument which should be a vector of scalar valued functions, intended to represent a vector valued function and returns a scalar value. It should satisfy the defining relation: divergence(F) = \partial(F_(x_1))/\partial(x_1) + ... + \partial(F_(x_n))/\partial(x_n)
Content MathML
<apply>
<divergence/>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>div</mo><mo/><mfenced open="(" close=")" separators=","><mi>a</mi></mfenced>
</mrow>Default Rendering: Image
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
Content MathML
<apply>
<divergence/>
<ci type="vector">E</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>div</mo><mo/><mfenced open="(" close=")" separators=","><mi>E</mi></mfenced>
</mrow>Default Rendering: Image
Content MathML
<apply>
<divergence/>
<bvar>
<ci>x</ci>
</bvar>
<bvar>
<ci>y</ci>
</bvar>
<bvar>
<ci>z</ci>
</bvar>
<vector>
<apply>
<plus/>
<ci>x</ci>
<ci>y</ci>
</apply>
<apply>
<plus/>
<ci>x</ci>
<ci>z</ci>
</apply>
<apply>
<plus/>
<ci>z</ci>
<ci>y</ci>
</apply>
</vector>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>div</mo><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mo>,</mo><mi>y</mi><mo>,</mo><mi>z</mi><mrow>
<mo>(</mo><mtable>
<mtr><mtd><mrow>
<mi>x</mi><mo>+</mo><mi>y</mi>
</mrow></mtd></mtr><mtr><mtd><mrow>
<mi>x</mi><mo>+</mo><mi>z</mi>
</mrow></mtd></mtr><mtr><mtd><mrow>
<mi>z</mi><mo>+</mo><mi>y</mi>
</mrow></mtd></mtr>
</mtable><mo>)</mo>
</mrow>
</mfenced>
</mrow>Default Rendering: Image
Content MathML
<apply>
<eq/>
<apply>
<divergence/>
<ci type="vectorfield">a</ci>
</apply>
<apply>
<limit/>
<bvar>
<ci>V</ci>
</bvar>
<condition>
<apply>
<tendsto/>
<ci>V</ci>
<cn>0</cn>
</apply>
</condition>
<apply>
<divide/>
<apply>
<int definitionURL="SurfaceIntegrals.htm" encoding="text"/>
<bvar>
<ci>S</ci>
</bvar>
<ci>a</ci>
</apply>
<ci>V</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mrow>
<mo>div</mo><mo/><mfenced open="(" close=")" separators=","><mi>a</mi></mfenced>
</mrow><mo>=</mo><mrow>
<munder>
<mi>lim</mi><mrow>
<mi>V</mi><mo>→</mo><mn>0</mn>
</mrow>
</munder><mrow>
<mrow>
<msubsup>
<mi>∫</mi><mrow/><mrow/>
</msubsup><mi>a</mi><mo>d</mo><mi>S</mi>
</mrow><mo>/</mo><mi>V</mi>
</mrow>
</mrow>
</mrow>Default Rendering: Image
4.3.13.5 Gradient (grad)
The grad element is the vector calculus gradient operator, often called
grad.
This symbol is used to represent the grad function. It takes one argument which should be a scalar valued function and returns a vector of functions. It should satisfy the defining relation: grad(F) = (\partial(F)/\partial(x_1), ... ,\partial(F)/partial(x_n))
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
Content MathML
<apply>
<grad/>
<ci type="function"> f</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>grad</mo><mo/><mfenced open="(" close=")" separators=","><mi> f</mi></mfenced>
</mrow>Default Rendering: Image
Content MathML
<apply>
<grad/>
<bvar>
<ci>x</ci>
</bvar>
<bvar>
<ci>y</ci>
</bvar>
<bvar>
<ci>z</ci>
</bvar>
<apply>
<times/>
<ci>x</ci>
<ci>y</ci>
<ci>z</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>grad</mo><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mo>,</mo><mi>y</mi><mo>,</mo><mi>z</mi><mrow>
<mi>x</mi><mo/><mi>y</mi><mo/><mi>z</mi>
</mrow>
</mfenced>
</mrow>Default Rendering: Image
4.3.13.6 Curl (curl)
This symbol is used to represent the curl function. It takes one argument which should be a vector of scalar valued functions, intended to represent a vector valued function and returns a vector of functions. It should satisfy the defining relation: curl(F) = i X \partial(F)/\partial(x) + j X \partial(F)/\partial(y) + j X \partial(F)/\partial(Z) where i,j,k are the unit vectors corresponding to the x,y,z axes respectively and the multiplication X is cross multiplication.
Content MathML
<apply>
<curl/>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>curl</mo><mo/><mfenced open="(" close=")" separators=","><mi>a</mi></mfenced>
</mrow>Default Rendering: Image
Content MathML
<apply>
<curl/>
<ci type="vector">f</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>curl</mo><mo/><mfenced open="(" close=")" separators=","><mi>f</mi></mfenced>
</mrow>Default Rendering: Image
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
| Editorial note: MiKo | |
| We do not seem to have a binding curl example, maybe we should come up with one | |
4.3.13.7 Laplacian (laplacian)
Content MathML
<apply>
<laplacian/>
<ci type="vector">E</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<msup>
<mo>∇</mo><mn>2</mn>
</msup><mo/><mfenced open="(" close=")" separators=","><mi>E</mi></mfenced>
</mrow>Default Rendering: Image
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
Content MathML
<apply>
<laplacian/>
<bvar>
<ci>x</ci>
</bvar>
<bvar>
<ci>y</ci>
</bvar>
<bvar>
<ci>z</ci>
</bvar>
<apply>
<ci>f</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<msup>
<mo>∇</mo><mn>2</mn>
</msup><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mo>,</mo><mi>y</mi><mo>,</mo><mi>z</mi><mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mi>y</mi>
</mfenced>
</mrow>
</mfenced>
</mrow>Default Rendering: Image
Content MathML
<apply>
<eq/>
<apply>
<laplacian/>
<ci>f</ci>
</apply>
<apply>
<divergence/>
<apply>
<grad/>
<ci>f</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<mrow>
<msup>
<mo>∇</mo><mn>2</mn>
</msup><mo/><mfenced open="(" close=")" separators=","><mi>f</mi></mfenced>
</mrow><mo>=</mo><mrow>
<mo>div</mo><mo/><mfenced open="(" close=")" separators=","><mrow>
<mo>grad</mo><mo/><mfenced open="(" close=")" separators=","><mi>f</mi></mfenced>
</mrow></mfenced>
</mrow>
</mrow>Default Rendering: Image
4.3.14 Theory of Sets
4.3.14.1 Set (set)
This symbol represents the set construct. It is an n-ary function. The set entries are given explicitly. There is no implied ordering to the elements of a set.
Content MathML
<set>
<ci>a</ci>
<ci>b</ci>
<ci>c</ci>
</set>Default Rendering: Presentation MathML
<mrow>
<mo>{</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>}</mo>
</mrow>Default Rendering: Image
In general a set can be constructed by providing a function and a domain of application. The elements of the set correspond to the values obtained by evaluating the function at the points of the domain.
Content MathML
<set>
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<lt/>
<ci>x</ci>
<cn>5</cn>
</apply>
</condition>
</set>Default Rendering: Presentation MathML
<mrow>
<mo>{</mo><mi>x</mi><mo>|</mo><mrow>
<mi>x</mi><mo><<!--LESS-THAN SIGN--></mo><mn>5</mn>
</mrow><mo>}</mo>
</mrow>Default Rendering: Image
Content MathML
<set>
<bvar>
<ci type="set">S</ci>
</bvar>
<condition>
<apply>
<in/>
<ci>S</ci>
<ci type="list">T</ci>
</apply>
</condition>
<ci>S</ci>
</set>Default Rendering: Presentation MathML
<mrow>
<mo>{</mo><mi>S</mi><mo>|</mo><mrow>
<mi>S</mi><mo>∈</mo><mi>T</mi>
</mrow><mo>}</mo>
</mrow>Default Rendering: Image
Content MathML
<set>
<bvar>
<ci> x </ci>
</bvar>
<condition>
<apply>
<and/>
<apply>
<lt/>
<ci> x </ci>
<cn> 5 </cn>
</apply>
<apply>
<in/>
<ci> x </ci>
<naturalnumbers/>
</apply>
</apply>
</condition>
<ci> x </ci>
</set>Default Rendering: Presentation MathML
<mrow>
<mo>{</mo><mi> x </mi><mo>|</mo><mrow>
<mrow>
<mo>(</mo><mi> x </mi><mo><<!--LESS-THAN SIGN--></mo><mn> 5 </mn><mo>)</mo>
</mrow><mo>∧</mo><mrow>
<mi> x </mi><mo>∈</mo><mi mathvariant="double-struck">N</mi>
</mrow>
</mrow><mo>}</mo>
</mrow>Default Rendering: Image
In strict MathML, this usage represented with the suchthat symbol from the set1 content dictionary.
If the type has value "multiset", then the set and suchthat from the
multiset1 should be used instead.
4.3.14.2 List (list)
This symbol denotes the list construct which is an n-ary function. The list entries must be given explicitly.
Content MathML
<list>
<ci>a</ci>
<ci>b</ci>
<ci>c</ci>
</list>Default Rendering: Presentation MathML
<mrow> <mo>(</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>)</mo> </mrow>
Default Rendering: Image
In general a list can be constructed by providing a function and a domain of application. The elements of the list correspond to the values obtained by evaluating the function at the points of the domain.
This symbol represents the suchthat function which may be used to construct lists, it takes two arguments. The first argument should be the set which contains the elements of the list, the second argument should be a predicate, that is a function from the set to the booleans which describes if an element is to be in the list returned.
Content MathML
<list order="numeric">
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<lt/>
<ci>x</ci>
<cn>5</cn>
</apply>
</condition>
</list>Default Rendering: Presentation MathML
<mrow>
<mo>(</mo><mi>x</mi><mo>|</mo><mrow>
<mi>x</mi><mo><<!--LESS-THAN SIGN--></mo><mn>5</mn>
</mrow><mo>)</mo>
</mrow>Default Rendering: Image
An order attribute can be used to specify what ordering is to be
used. When the nature of the child elements permits, the ordering defaults to a numeric
or lexicographic ordering.
Lists differ from sets in that there is an explicit order to the elements. Two orders
are supported: lexicographic and numeric. The kind of ordering that should be used is
specified by the order attribute.
4.3.14.3 Union (union)
This symbol is used to denote the n-ary union of sets. It takes sets as arguments, and denotes the set that contains all the elements that occur in any of them.
Content MathML
<apply>
<union/>
<ci>A</ci>
<ci>B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>∪</mo><mi>B</mi> </mrow>
Default Rendering: Image
The union operator element can be used as a binding operator in
pragmatic Content MathML. This role is taken over by the big_union symbol in
strict Content MathML.
<apply>
<union/>
<bvar><ci>x</ci></bvar>
<apply><interval/><cn>0</cn><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="set1">big_union</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="interval1">integer_interval</csymbol><cn>0</cn><ci>x</ci></apply>
</bind>
</apply>This n-ary operator is used to construct the union over a collection of sets.
Content MathML
<apply>
<union/>
<bvar>
<ci type="set">S</ci>
</bvar>
<domainofapplication>
<ci type="list">L</ci>
</domainofapplication>
<ci type="set"> S</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>S</mi><mo>∪</mo><merror/><mo>∪</mo><mi> S</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the union and big_union from the
multiset1 should be used instead.
4.3.14.4 Intersect (intersect)
This symbol is used to denote the n-ary intersection of sets. It takes sets as arguments, and denotes the set that contains all the elements that occur in all of them.
Content MathML
<apply>
<intersect/>
<ci type="set"> A</ci>
<ci type="set"> B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi> A</mi><mo>∩</mo><mi> B</mi> </mrow>
Default Rendering: Image
The intersect operator element can be used as a binding operator in
pragmatic Content MathML. This role is taken over by the big_intersect
symbol in strict Content MathML.
<apply>
<intersect/>
<bvar><ci>x</ci></bvar>
<apply><interval/><cn>0</cn><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="set1">big_intersect</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="interval1">integer_interval</csymbol><cn>0</cn><ci>x</ci></apply>
</bind>
</apply>This n-ary operator is used to construct the intersection over a collection of sets.
Content MathML
<apply>
<intersect/>
<ci type="list">L</ci>
<bind>
<lambda/>
<bvar>
<ci type="set"> S</ci>
</bvar>
<ci type="set"> S</ci>
</bind>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>L</mi><mo>∩</mo><mrow> <mrow> <mi>λ</mi><mrow/><mo>.</mo><mfenced/> </mrow><mo>.</mo><mi> S</mi> </mrow> </mrow>
Default Rendering: Image
If the type has value "multiset", then the intersect and big_intersect
from the multiset1 should be used instead.
4.3.14.5 Set inclusion (in)
This symbol has two arguments, an element and a set. It is used to denote that the element is in the given set.
Content MathML
<apply>
<in/>
<ci>a</ci>
<ci type="set">A</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>∈</mo><mi>A</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the in from the multiset1 should be used instead.
4.3.14.6 Set exclusion (notin)
This symbol has two arguments, an element and a set. It is used to denote that the element is not in the given set.
Content MathML
<apply>
<notin/>
<ci>a</ci>
<ci type="set">A</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>a</mi><mo>∉</mo><mi>A</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the notin from the multiset1 should be used
instead.
4.3.14.7 Subset (subset)
This symbol has two (set) arguments. It is used to denote that the first set is a subset of the second.
Content MathML
<apply>
<subset/>
<ci type="set">A</ci>
<ci type="set">B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>⊆</mo><mi>B</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the subset from the multiset1 should be used
instead.
| Editorial note: MiKo | |
| There is a version with bvar here, what to do here? | |
4.3.14.8 Proper Subset (prsubset)
This symbol has two (set) arguments. It is used to denote that the first set is a proper subset of the second, that is a subset of the second set but not actually equal to it.
Content MathML
<apply>
<prsubset/>
<ci type="set">A</ci>
<ci type="set">B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>⊂</mo><mi>B</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the prsubset from the multiset1 should be used
instead.
| Editorial note: MiKo | |
| There is a version with bvar here, what to do here? | |
4.3.14.9 Not Subset (notsubset)
This symbol has two (set) arguments. It is used to denote that the first set is not a subset of the second.
Content MathML
<apply>
<notsubset/>
<ci type="set">A</ci>
<ci type="set">B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>⊈</mo><mi>B</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the notsubset from the multiset1 should be used
instead.
4.3.14.10 Not Proper Subset (notprsubset)
This symbol has two (set) arguments. It is used to denote that the first set is not a proper subset of the second. A proper subset of a set is a subset of the set but not actually equal to it.
Content MathML
<apply>
<notprsubset/>
<ci type="set">A</ci>
<ci type="set">B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>⊄</mo><mi>B</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the notprsubset from the multiset1 should be used
instead.
4.3.14.11 Set Difference (setdiff)
This symbol is used to denote the set difference of two sets. It takes two sets as arguments, and denotes the set that contains all the elements that occur in the first set, but not in the second.
Content MathML
<apply>
<setdiff/>
<ci type="set">A</ci>
<ci type="set">B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>∖</mo><mi>B</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the setdiff from the multiset1 should be used
instead.
4.3.14.12 Cardinality (card)
This symbol is used to denote the number of elements in a set. It is either a non-negative integer, or an infinite cardinal number. The symbol infinity may be used for an unspecified infinite cardinal.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
If the type has value "multiset", then the size from the multiset1 should be used
instead.
4.3.14.13 Cartesian product (cartesianproduct)
Content MathML
<apply>
<cartesianproduct/>
<ci>A</ci>
<ci>B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>×</mo><mi>B</mi> </mrow>
Default Rendering: Image
If the type has value "multiset", then the cartesianproduct from the multiset1 should be used
instead.
| Editorial note: MiKo | |
| There is a version with bvar here, what to do here? | |
4.3.15 Sequences and Series
4.3.15.1 Sum (sum)
An operator taking two arguments, the first being the range of summation, e.g. an integral interval, the second being the function to be summed. Note that the sum may be over an infinite interval.
In pragmatic Content MathML, the sum operator may used as the first child of
an apply element, which is qualified by providing a
domainofapplication, an uplimit, lowlimit pair,
condition element. The index for the summation is specified by a bvar
element.
If no bound variables are specified then terms of the sum correspond to those
produced by evaluating the function that is provided at the points of the domain, while
if bound variables are present they are the index of summation and they take on the
values of points in the domain. In this case the terms of the sum correspond to the
values of the expression that is provided, evaluated at those points. Depending on the
structure of the domain, the domain of summation can be abbreviated by using
uplimit and lowlimit to specify upper and lower limits for the
sum.
A sum in pragmatic Content MathML is turned into strict Content MathML by
supplying a lambda binder for the expression to make it into a function. The
range of integration is converted to an interval.
<apply>
<sum/>
<bvar><ci>i</ci></bvar>
<lowlimit><cn>0</cn></lowlimit>
<uplimit><cn>100</cn></uplimit>
<apply><power/><ci>x</ci><ci>i</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">sum</csymbol>
<apply>
<csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>Content MathML
<apply>
<sum/>
<bind>
<lambda/>
<bvar>
<ci>x</ci>
</bvar>
<lowlimit>
<ci>a</ci>
</lowlimit>
<uplimit>
<ci>b</ci>
</uplimit>
<apply>
<ci>f</ci>
<ci>x</ci>
</apply>
</bind>
</apply>Default Rendering: Presentation MathML
<mrow>
<msubsup>
<mo>∑</mo><mrow/><mrow/>
</msubsup><mrow>
<mrow>
<mi>λ</mi><mrow/><mo>.</mo><mfenced/>
</mrow><mo>.</mo><mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=","><mi>x</mi></mfenced>
</mrow>
</mrow>
</mrow>Default Rendering: Image
Content MathML
<apply>
<sum/>
<bind>
<lambda/>
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<in/>
<ci>x</ci>
<ci type="set">B</ci>
</apply>
</condition>
<apply>
<ci type="function"> f</ci>
<ci>x</ci>
</apply>
</bind>
</apply>Default Rendering: Presentation MathML
<mrow>
<msubsup>
<mo>∑</mo><mrow/><mrow/>
</msubsup><mrow>
<mrow>
<mi>λ</mi><mrow/><mo>.</mo><mfenced/>
</mrow><mo>.</mo><mrow>
<mi>x</mi><mo>∈</mo><mi>B</mi>
</mrow><mrow>
<mi> f</mi><mo/><mfenced open="(" close=")" separators=","><mi>x</mi></mfenced>
</mrow>
</mrow>
</mrow>Default Rendering: Image
Content MathML
<apply>
<sum/>
<domainofapplication>
<ci type="set">B</ci>
</domainofapplication>
<ci type="function">f</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <msubsup> <mo>∑</mo><mrow/><mrow/> </msubsup><mi>f</mi> </mrow>
Default Rendering: Image
4.3.15.2 Product (product)
An operator taking two arguments, the first being the range of multiplication e.g. an integral interval, the second being the function to be multiplied. Note that the product may be over an infinite interval.
In pragmatic Content MathML, the product Operator may used as the first
child of an apply element, which is qualified by providing a
domainofapplication, an uplimit, lowlimit pair,
condition element. The index is specified by a bvar element.
If no bound variables are specified then terms of the product correspond to those
produced by evaluating the function that is provided at the points of the domain, while
if bound variables are present they are the index and they take on the values of points
in the domain. In this case the terms of the product correspond to the values of the
expression that is provided, evaluated at those points. Depending on the structure of
the domain, the domain of multiplication can be abbreviated by using uplimit
and lowlimit to specify upper and lower limits for the product.
A product in pragmatic Content MathML is turned into strict Content MathML
by supplying a lambda binder for the expression to make it into a function. The
range of integration is converted to an interval.
<apply>
<product/>
<bvar><ci>i</ci></bvar>
<apply><power/><ci>x</ci><ci>i</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="arith1">product</csymbol>
<apply>
<csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>Content MathML
<apply>
<product/>
<bind>
<lambda/>
<bvar>
<ci>x</ci>
</bvar>
<lowlimit>
<ci>a</ci>
</lowlimit>
<uplimit>
<ci>b</ci>
</uplimit>
<apply>
<ci type="function"> f</ci>
<ci>x</ci>
</apply>
</bind>
</apply>Default Rendering: Presentation MathML
<mrow>
<msubsup>
<mo>∏</mo><mrow/><mrow/>
</msubsup><mrow>
<mrow>
<mi>λ</mi><mrow/><mo>.</mo><mfenced/>
</mrow><mo>.</mo><mrow>
<mi> f</mi><mo/><mfenced open="(" close=")" separators=","><mi>x</mi></mfenced>
</mrow>
</mrow>
</mrow>Default Rendering: Image
Content MathML
<apply>
<product/>
<bind>
<lambda/>
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<in/>
<ci>x</ci>
<ci type="set">B</ci>
</apply>
</condition>
<apply>
<ci>f</ci>
<ci>x</ci>
</apply>
</bind>
</apply>Default Rendering: Presentation MathML
<mrow>
<msubsup>
<mo>∏</mo><mrow/><mrow/>
</msubsup><mrow>
<mrow>
<mi>λ</mi><mrow/><mo>.</mo><mfenced/>
</mrow><mo>.</mo><mrow>
<mi>x</mi><mo>∈</mo><mi>B</mi>
</mrow><mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=","><mi>x</mi></mfenced>
</mrow>
</mrow>
</mrow>Default Rendering: Image
4.3.15.3 Limits (limit)
This symbol is used to denote the limit of a function. It takes 3 arguments: the limiting value of the argument, the method of approach (either null, above, below or both_sides) and the function.
The limit element represents the operation of taking a limit of a
sequence. The limit point is expressed by specifying a lowlimit and a
bvar, or by specifying a condition on one or more bound variables.
Content MathML
<apply>
<limit/>
<bvar>
<ci>x</ci>
</bvar>
<lowlimit>
<cn>0</cn>
</lowlimit>
<apply>
<sin/>
<ci>x</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow>
<munder>
<mi>lim</mi><mrow>
<mi>x</mi>
<mo>→</mo>
<mn>0</mn>
</mrow>
</munder><mrow>
<mi>sin</mi><mi>x</mi>
</mrow>
</mrow>Default Rendering: Image
Content MathML
<apply>
<limit/>
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<tendsto/>
<ci>x</ci>
<cn>0</cn>
</apply>
</condition>
<apply>
<sin/>
<ci>x</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow> <munder> <mi>lim</mi><mrow> <mi>x</mi><mo>→</mo><mn>0</mn> </mrow> </munder><mrow> <mi>sin</mi><mi>x</mi> </mrow> </mrow>
Default Rendering: Image
Content MathML
<apply>
<limit/>
<bvar>
<ci>x</ci>
</bvar>
<condition>
<apply>
<tendsto type="above"/>
<ci>x</ci>
<ci>a</ci>
</apply>
</condition>
<apply>
<sin/>
<ci>x</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow> <munder> <mi>lim</mi><mrow> <mi>x</mi><mo>→</mo><mi>a</mi> </mrow> </munder><mrow> <mi>sin</mi><mi>x</mi> </mrow> </mrow>
Default Rendering: Image
The direction from which a limiting value is approached is given as an argument
limit in strict content MathML, which supplies the
direction specifier symbols both_sides, above, and below for this
purpose. The first correspond to the values "all", "above",
and "below" of the type attribute of the tendsto
element below. The null symbol corresponds to the case
where no type attribute is present. We translate
<apply><limit/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><tendsto/><ci>x</ci><cn>0</cn></apply>
</condition>
<apply><sin/><ci>x</ci></apply>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="limit1">limit</csymbol>
<ci>0</ci>
<csymbol cd="limit">null</csymbol>
<bind>
<csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>4.3.15.4 Tends To (tendsto)
This symbol is also used to express the relation that a quantity is tending to a specified value. While this is used primarily as part of the statement of a mathematical limit, it exists as a construct on its own to allow one to capture mathematical statements such as "As x tends to y," and to provide a building block to construct more general kinds of limits.
The tendsto element takes the attributes type to set the
direction from which the limiting value is approached.
Content MathML
<apply>
<tendsto type="above"/>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
<apply>
<power/>
<ci>a</ci>
<cn>2</cn>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow> <msup> <mi>x</mi><mn>2</mn> </msup><mo>→</mo><msup> <mi>a</mi><mn>2</mn> </msup> </mrow>
Default Rendering: Image
Content MathML
<apply>
<tendsto/>
<vector>
<ci>x</ci>
<ci>y</ci>
</vector>
<vector>
<apply>
<ci type="function">f</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
<apply>
<ci type="function">g</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</vector>
</apply>Default Rendering: Presentation MathML
<mrow>
<mrow>
<mo>(</mo><mtable>
<mtr><mtd><mi>x</mi></mtd></mtr><mtr><mtd><mi>y</mi></mtd></mtr>
</mtable><mo>)</mo>
</mrow><mo>→</mo><mrow>
<mo>(</mo><mtable>
<mtr><mtd><mrow>
<mi>f</mi><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mi>y</mi>
</mfenced>
</mrow></mtd></mtr><mtr><mtd><mrow>
<mi>g</mi><mo/><mfenced open="(" close=")" separators=",">
<mi>x</mi><mi>y</mi>
</mfenced>
</mrow></mtd></mtr>
</mtable><mo>)</mo>
</mrow>
</mrow>Default Rendering: Image
4.3.16 Elementary classical functions
4.3.16.1 common trigonometric functions
The names of the common trigonometric functions supported by MathML are listed below. Since their standard interpretations are widely known, they are discussed as a group.
sin |
cos |
tan |
sec |
csc |
cot |
sinh |
cosh |
tanh |
sech |
csch |
coth |
arcsin |
arccos |
arctan |
arccosh |
arccot |
arccoth |
arccsc |
arccsch |
arcsec |
arcsech |
arcsinh |
arctanh |
These operator elements denote the standard trigonometric functions.
Content MathML
<apply>
<sin/>
<ci>x</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>sin</mi><mi>x</mi> </mrow>
Default Rendering: Image
Content MathML
<apply>
<sin/>
<apply>
<plus/>
<apply>
<cos/>
<ci>x</ci>
</apply>
<apply>
<power/>
<ci>x</ci>
<cn>3</cn>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>sin</mi><mrow> <mo>(</mo><mrow> <mi>cos</mi><mi>x</mi> </mrow><mo>+</mo><msup> <mi>x</mi><mn>3</mn> </msup><mo>)</mo> </mrow> </mrow>
Default Rendering: Image
4.3.16.2 Exponential (exp)
This symbol represents the exponentiation function associated with the inverse of the ln function as described in Abramowitz and Stegun, section 4.2. It takes one argument.
Content MathML
<apply>
<exp/>
<ci>x</ci>
</apply>Default Rendering: Presentation MathML
<msup> <mi>e</mi><mi>x</mi> </msup>
Default Rendering: Image
4.3.16.3 Natural Logarithm (ln)
This symbol represents the ln function (natural logarithm) as described in Abramowitz and Stegun, section 4.1. It takes one argument. Note the description in the CMP/FMP of the branch cut. If signed zeros are in use, the inequality needs to be non-strict.
Content MathML
<apply>
<ln/>
<ci>a</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>ln</mi><mi>a</mi> </mrow>
Default Rendering: Image
4.3.16.4 Logarithm (log)
This symbol represents a binary log function; the first argument is the base, to which the second argument is log'ed. It is defined in Abramowitz and Stegun, Handbook of Mathematical Functions, section 4.1
Content MathML
<apply>
<log/>
<logbase>
<cn>3</cn>
</logbase>
<ci>x</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <msub> <mi>log</mi><mn>3</mn> </msub><mi>x</mi> </mrow>
Default Rendering: Image
Content MathML
<apply>
<log/>
<ci>x</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>log</mi><mi>x</mi> </mrow>
Default Rendering: Image
4.3.17 Statistics
4.3.17.1 Mean (mean)
mean is the operator element representing a mean or average of a
data set or random variable. If it is used on a data set, then the mean element
corresponds to the mean from the s_data1
content dictionary, if it is used on a random variable, then it corresponds to the
mean from the s_dist1 CD.
Content MathML
<apply>
<mean/>
<cn>3</cn>
<cn>4</cn>
<cn>3</cn>
<cn>7</cn>
<cn>4</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>〈</mo><mn>3</mn><mo>,</mo><mn>4</mn><mo>,</mo><mn>3</mn><mo>,</mo><mn>7</mn><mo>,</mo><mn>4</mn><mo>〉</mo> </mrow>
Default Rendering: Image
Content MathML
<apply>
<mean/>
<ci type="discrete_random_variable">X</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mo>〈</mo><mi>X</mi><mo>〉</mo> </mrow>
Default Rendering: Image
4.3.17.2 Standard Deviation (sdev)
mean is the operator element representing the standard deviation of a data set
or random variable. If it is used on a data set, then the sdev element
corresponds to the sdev from the s_data1
content dictionary, if it is used on a random variable, then it corresponds to the
sdev from the s_dist1 CD.
Content MathML
<apply>
<sdev/>
<cn>3</cn>
<cn>4</cn>
<cn>2</cn>
<cn>2</cn>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>σ</mo><mo/><mfenced open="(" close=")" separators=",">
<mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn>
</mfenced>
</mrow>Default Rendering: Image
Content MathML
<apply>
<sdev/>
<ci type="discrete_random_variable">X</ci>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>σ</mo><mo/><mfenced open="(" close=")" separators=","><mi>X</mi></mfenced>
</mrow>Default Rendering: Image
4.3.17.3 Variance (variance)
variance is the operator element representing the standard deviation of a data
set or random variable. If it is used on a data set, then the variance element
corresponds to the variance from the s_data1
content dictionary, if it is used on a random variable, then it corresponds to the
variance from the s_dist1 CD.
Content MathML
<apply>
<variance/>
<cn>3</cn>
<cn>4</cn>
<cn>2</cn>
<cn>2</cn>
</apply>Default Rendering: Presentation MathML
<msup> <mrow> <mo>σ</mo><mo>(</mo><mn>3</mn><mo>)</mo> </mrow><mn>2</mn> </msup>
Default Rendering: Image
Content MathML
<apply>
<variance/>
<ci type="discrete_random_variable"> X</ci>
</apply>Default Rendering: Presentation MathML
<msup> <mrow> <mo>σ</mo><mo>(</mo><mi> X</mi><mo>)</mo> </mrow><mn>2</mn> </msup>
Default Rendering: Image
4.3.17.4 Median (median)
This symbol represents an n-ary function denoting the median of its arguments. That is, if the data were placed in ascending order then it denotes the middle one (in the case of an odd amount of data) or the average of the middle two (in the case of an even amount of data). See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
Content MathML
<apply>
<median/>
<cn>3</cn>
<cn>4</cn>
<cn>2</cn>
<cn>2</cn>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>median</mo><mo/><mfenced open="(" close=")" separators=",">
<mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn>
</mfenced>
</mrow>Default Rendering: Image
4.3.17.5 Mode (mode)
This symbol represents an n-ary function denoting the mode of its arguments. That is the value which occurs with the greatest frequency. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
Content MathML
<apply>
<mode/>
<cn>3</cn>
<cn>4</cn>
<cn>2</cn>
<cn>2</cn>
</apply>Default Rendering: Presentation MathML
<mrow>
<mo>mode</mo><mo/><mfenced open="(" close=")" separators=",">
<mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn>
</mfenced>
</mrow>Default Rendering: Image
4.3.17.6 Moment (moment, momentabout)
moment s used to denote the i'th moment of a set of data set or random
variable. If it is used on a data set, then the moment element corresponds to the
moment from the s_data1 content
dictionary
This symbol is used to denote the i'th moment of a set of data. The first argument should be the degree of the moment (that is, for the i'th moment the first argument should be i), the second argument should be the point about which the moment is being taken and the rest of the arguments are treated as the data. For n data values x_1, x_2, ..., x_n the i'th moment about c is (1/n) ((x_1-c)^i + (x_2-c)^i + ... + (x_n-c)^i). See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1.
if it is used on a random variable, then it corresponds to the moment from the s_dist1 CD.
This symbol represents a ternary function to denote the i'th moment of a distribution. The first argument should be the degree of the moment (that is, for the i'th moment the first argument should be i), the second argument is the value about which the moment is to be taken and the third argument is a univariate function to describe the distribution. That is, if f is the function which describe the distribution. The i'th moment of f about a is the integral of (x-a)^i*f(x) with respect to x, over the interval (-infinity,infinity). See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, section 7.7.1
In pragmatic content MathML we use the qualifier degree for the n
in " n-th moment" and the qualifier momentabout for the
p in "moment about p". We translate:
<apply>
<moment/>
<degree><cn>3</cn></degree>
<momentabout><ci>p</ci></momentabout>
<ci>X</ci>
</apply>Strict MathML equivlalent
<apply>
<csymbol cd="s_dist">moment</csymbol>
<cn>3</cn>
<ci>p</ci>
<ci>X</ci>
</apply>The moment function accepts the degree and momentabout
schema. If present, the degree schema denotes the order of the moment. Otherwise,
the moment is assumed to be the first order moment. When used with moment, the
degree schema is expected to contain a single child schema; otherwise an error is
generated. If present, the momentabout schema denotes the point about which the
moment is taken. Otherwise, the moment is assumed to be the moment about zero.
Content MathML
<apply>
<moment/>
<degree>
<cn>3</cn>
</degree>
<momentabout>
<mean/>
</momentabout>
<cn>6</cn>
<cn>4</cn>
<cn>2</cn>
<cn>2</cn>
<cn>5</cn>
</apply>Default Rendering: Presentation MathML
<msub> <mrow> <mo>〈</mo><msup> <mn>5</mn><mn>3</mn> </msup><mo>〉</mo> </mrow><mi>mean</mi> </msub>
Default Rendering: Image
Content MathML
<apply>
<moment/>
<degree>
<cn>3</cn>
</degree>
<momentabout>
<ci>p</ci>
</momentabout>
<ci>X</ci>
</apply>Default Rendering: Presentation MathML
<msub> <mrow> <mo>〈</mo><msup> <mi>X</mi><mn>3</mn> </msup><mo>〉</mo> </mrow><mi>p</mi> </msub>
Default Rendering: Image
4.3.18 Linear Algebra
4.3.18.1 Vector (vector)
A vector is an ordered n-tuple of values representing an element of an n-dimensional vector space. The "values" are all from the same ring, typically real or complex. Where orientation is important, such as for pre or post multiplication by a matrix a vector is treated as a row vector and its transpose is treated a column vector. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.4]
For purposes of interaction with matrices and matrix multiplication, vectors are regarded as equivalent to a matrix consisting of a single column, and the transpose of a vector behaves the same as a matrix consisting of a single row. Note that vectors may be rendered either as a single column or row.
vector is a constructor element (see ??? ).
Content MathML
<vector>
<apply>
<plus/>
<ci>x</ci>
<ci>y</ci>
</apply>
<cn>3</cn>
<cn>7</cn>
</vector>Default Rendering: Presentation MathML
<mrow>
<mo>(</mo><mtable>
<mtr><mtd><mrow>
<mi>x</mi><mo>+</mo><mi>y</mi>
</mrow></mtd></mtr><mtr><mtd><mn>3</mn></mtd></mtr><mtr><mtd><mn>7</mn></mtd></mtr>
</mtable><mo>)</mo>
</mrow>Default Rendering: Image
In general a vector can be constructed by providing a function and a 1-dimensional domain of application. The entries of the vector correspond to the values obtained by evaluating the function at the points of the domain.
The vector element constructs vectors from an n-dimensional
vector space so that its n child elements typically represent real or complex
valued scalars as in the three-element vector
This symbol allows to construct a vector by providing a function and a 1-dimensional domain of application. The entries of the vector correspond to the values obtained by evaluating the function at the points of the domain.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.18.2 Matrix (matrix)
A vector is an ordered n-tuple of values representing an element of an n-dimensional vector space. The "values" are all from the same ring, typically real or complex. Where orientation is important, such as for pre or post multiplication by a matrix a vector is treated as a row vector and its transpose is treated a column vector. See CRC Standard Mathematical Tables and Formulae, editor: Dan Zwillinger, CRC Press Inc., 1996, [2.4]
For purposes of interaction with matrices and matrix multiplication, vectors are regarded as equivalent to a matrix consisting of a single column, and the transpose of a vector behaves the same as a matrix consisting of a single row. Note that vectors may be rendered either as a single column or row.
Note that the behavior of the matrix and matrixrow elements is
substantially different from the mtable and mtr presentation
elements.
matrix is a constructor element (see ??? ).
In general a matrix can be constructed by providing a function and a 2-dimensional
domain of application. The entries of the matrix correspond to the values obtained by
evaluating the function at the points of the domain. The qualifications defined by a
domainofapplication element can also be abbreviated in several ways including
a condition element placing constraints directly on bound variables and an
expression in those variables.
This symbol allows to construct a matrix by providing a function and a 2-dimensional domain of application. The entries of the matrix correspond to the values obtained by evaluating the function at the points of the domain.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.18.3 Matrix row (matrixrow)
This symbol is an n-ary constructor used to represent rows of matrices. Its arguments should be members of a ring.
Matrix rows are not directly rendered by themselves outside of the context of a matrix.
4.3.18.4 Determinant (determinant)
This symbol denotes the unary function which returns the determinant of its argument, the argument should be a square matrix.
Content MathML
<apply>
<determinant/>
<ci type="matrix">A</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>det</mi><mi>A</mi> </mrow>
Default Rendering: Image
4.3.18.5 Transpose (transpose)
This symbol represents a unary function that denotes the transpose of the given matrix or vector.
Content MathML
<apply>
<transpose/>
<ci type="matrix">A</ci>
</apply>Default Rendering: Presentation MathML
<msup> <mi>A</mi><mi>T</mi> </msup>
Default Rendering: Image
4.3.18.6 Selector (selector)
The selector element is the operator for indexing into vectors matrices
and lists. It accepts one or more arguments. The first argument identifies the vector,
matrix or list from which the selection is taking place, and the second and subsequent
arguments, if any, indicate the kind of selection taking place.
When selector is used with a single argument, it should be interpreted as
giving the sequence of all elements in the list, vector or matrix given. The ordering
of elements in the sequence for a matrix is understood to be first by column, then by
row. That is, for a matrix ( ai,j), where the indices denote row
and column, the ordering would be a 1,1, a
1,2, ... a 2,1, a2,2
... etc.
When three arguments are given, the last one is ignored for a list or vector, and in the case of a matrix, the second and third arguments specify the row and column of the selected element.
When two arguments are given, and the first is a vector or list, the second argument specifies an element in the list or vector.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
Content MathML
<apply>
<selector/>
<ci type="vector">V</ci>
<cn>1</cn>
</apply>Default Rendering: Presentation MathML
<msub> <mi>V</mi><mn>1</mn> </msub>
Default Rendering: Image
Content MathML
<apply>
<eq/>
<apply>
<selector/>
<matrix>
<matrixrow>
<cn>1</cn>
<cn>2</cn>
</matrixrow>
<matrixrow>
<cn>3</cn>
<cn>4</cn>
</matrixrow>
</matrix>
<cn>1</cn>
</apply>
<matrixrow>
<cn>1</cn>
<cn>2</cn>
</matrixrow>
</apply>Default Rendering: Presentation MathML
<mrow>
<msub>
<mrow>
<mo>(</mo><mtable>
<mtr>
<mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd>
</mtr><mtr>
<mtd><mn>3</mn></mtd><mtd><mn>4</mn></mtd>
</mtr>
</mtable><mo>)</mo>
</mrow><mn>1</mn>
</msub><mo>=</mo><mtable><mtr>
<mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd>
</mtr></mtable>
</mrow>Default Rendering: Image
4.3.18.7 Vector product (vectorproduct)
This symbol represents the vector product function. It takes two three dimensional vector arguments and returns a three dimensional vector.
Content MathML
<apply>
<eq/>
<apply>
<vectorproduct/>
<ci type="vector"> A</ci>
<ci type="vector"> B</ci>
</apply>
<apply>
<times/>
<ci>a</ci>
<ci>b</ci>
<apply>
<sin/>
<ci>θ</ci>
</apply>
<ci type="vector"> N</ci>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mi> A</mi><mo>×</mo><mi> B</mi> </mrow><mo>=</mo><mrow> <mi>a</mi><mo/><mi>b</mi><mo/><mrow> <mi>sin</mi><mi>θ</mi> </mrow><mo/><mi> N</mi> </mrow> </mrow>
Default Rendering: Image
4.3.18.8 Scalar product (scalarproduct)
This symbol represents the scalar product function. It takes two vector arguments and returns a scalar value.
Content MathML
<apply>
<eq/>
<apply>
<scalarproduct/>
<ci type="vector"> A</ci>
<ci type="vector">B</ci>
</apply>
<apply>
<times/>
<ci>a</ci>
<ci>b</ci>
<apply>
<cos/>
<ci>θ</ci>
</apply>
</apply>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mi> A</mi><mo>.</mo><mi>B</mi> </mrow><mo>=</mo><mrow> <mi>a</mi><mo/><mi>b</mi><mo/><mrow> <mi>cos</mi><mi>θ</mi> </mrow> </mrow> </mrow>
Default Rendering: Image
4.3.18.9 Outer product (outerproduct)
This symbol represents the outer product function. It takes two vector arguments and returns a matrix.
Content MathML
<apply>
<outerproduct/>
<ci type="vector">A</ci>
<ci type="vector">B</ci>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>A</mi><mo>⊗</mo><mi>B</mi> </mrow>
Default Rendering: Image
4.3.19 Constant and Symbol Elements
This section explains the use of the Constant and Symbol elements.
4.3.19.1 integers (integers)
This symbol represents the set of integers, positive, negative and zero.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.19.2 reals (reals)
This symbol represents the set of real numbers.
Content MathML
<apply>
<in/>
<cn type="real"> 44.997</cn>
<reals/>
</apply>Default Rendering: Presentation MathML
<mrow> <mn> 44.997</mn><mo>∈</mo><mi mathvariant="double-struck">R</mi> </mrow>
Default Rendering: Image
4.3.19.3 Rational Numbers (rationals)
This symbol represents the set of rational numbers.
Content MathML
<apply>
<in/>
<cn type="rational"> 22 <sep/>7</cn>
<rationals/>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mn> 22 </mn><mo>/</mo><mn>7</mn> </mrow><mo>∈</mo><mi mathvariant="double-struck">Q</mi> </mrow>
Default Rendering: Image
4.3.19.4 Natural Numbers (naturalnumbers)
This symbol represents the set of natural numbers (including zero).
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.19.5 complexes (complexes)
This symbol represents the set of complex numbers.
Content MathML
<apply>
<in/>
<cn type="complex">17<sep/>29</cn>
<complexes/>
</apply>Default Rendering: Presentation MathML
<mrow> <mn>1729</mn><mo>∈</mo><mi mathvariant="double-struck">C</mi> </mrow>
Default Rendering: Image
4.3.19.6 primes (primes)
This symbol represents the set of positive prime numbers.
Content MathML
<apply>
<in/>
<cn type="integer">17</cn>
<primes/>
</apply>Default Rendering: Presentation MathML
<mrow> <mn>17</mn><mo>∈</mo><mi mathvariant="double-struck">P</mi> </mrow>
Default Rendering: Image
4.3.19.7 Exponential e (exponentiale)
This symbol represents the base of the natural logarithm, approximately 2.718. See Abramowitz and Stegun, Handbook of Mathematical Functions, section 4.1.
Content MathML
<apply>
<eq/>
<apply>
<ln/>
<exponentiale/>
</apply>
<cn>1</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mi>ln</mi><mi>e</mi> </mrow><mo>=</mo><mn>1</mn> </mrow>
Default Rendering: Image
4.3.19.8 Imaginary i (imaginaryi)
This symbol represents the mathematical constant which is the square root of -1, commonly written i
Content MathML
<apply>
<eq/>
<apply>
<power/>
<imaginaryi/>
<cn>2</cn>
</apply>
<cn>-1</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <msup> <mi>i</mi><mn>2</mn> </msup><mo>=</mo><mn>-1</mn> </mrow>
Default Rendering: Image
4.3.19.9 Not A Number (notanumber)
A symbol to convey the notion of not-a-number. The result of an ill-posed floating computation. See IEEE standard for floating point representations.
Content MathML
Default Rendering: Presentation MathML
Default Rendering: Image
4.3.19.10 True (true)
This symbol represents the boolean value true, i.e. the logical constant for truth.
Content MathML
<apply>
<eq/>
<apply>
<or/>
<true/>
<ci type="boolean">P</ci>
</apply>
<true/>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mi>true</mi><mo>∨</mo><mi>P</mi> </mrow><mo>=</mo><mi>true</mi> </mrow>
Default Rendering: Image
4.3.19.11 False (false)
This symbol represents the boolean value false, i.e. the logical constant for falsehood.
Content MathML
<apply>
<eq/>
<apply>
<and/>
<false/>
<ci type="boolean">P</ci>
</apply>
<false/>
</apply>Default Rendering: Presentation MathML
<mrow> <mrow> <mi>false</mi><mo>∧</mo><mi>P</mi> </mrow><mo>=</mo><mi>false</mi> </mrow>
Default Rendering: Image
4.3.19.12 Empty Set (emptyset)
This symbol is used to represent the empty set, that is the set which contains no members. It takes no parameters.
The emptyset element takes an optional attribute type. If its
value is "multiset", then the emptyset corresponds to the
emptyset symbol from the multiset1 CD.
Content MathML
<apply>
<neq/>
<integers/>
<emptyset/>
</apply>Default Rendering: Presentation MathML
<mrow> <mi mathvariant="double-struck">Z</mi><mo>≠</mo><mi>∅</mi> </mrow>
Default Rendering: Image
4.3.19.13 pi (pi)
A symbol to convey the notion of pi, approximately 3.142. The ratio of the circumference of a circle to its diameter.
Content MathML
<apply>
<approx/>
<pi/>
<cn type="rational">22<sep/>7</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>π</mi><mo>≃</mo><mrow> <mn>22</mn><mo>/</mo><mn>7</mn> </mrow> </mrow>
Default Rendering: Image
4.3.19.14 Euler gamma (eulergamma)
A symbol to convey the notion of the gamma constant as defined in Abramowitz and Stegun, Handbook of Mathematical Functions, section 6.1.3. It is the limit of 1 + 1/2 + 1/3 + ... + 1/m - ln m as m tends to infinity, this is approximately 0.5772 15664.
Content MathML
<apply>
<approx/>
<eulergamma/>
<cn>0.5772156649</cn>
</apply>Default Rendering: Presentation MathML
<mrow> <mi>γ</mi><mo>≃</mo><mn>0.5772156649</mn> </mrow>
Default Rendering: Image
4.4 Deprecated content Elements
4.4.1 Declare (declare)
| Editorial note: MiKo | |
| This should maybe be moved into a general section about changes or deprecated elements. Also Stan thinks the text should be improved. | |
MathML2 provided the declare element that allowed to bind properties like
types to symbols and variables and to define abbreviations for structure sharing. This
element is deprecated in MathML 3. Structure sharing can obtained via the share
element (see Section 4.2.7 Structure Sharing (share) for details).
4.5 Rendering of Content Elements
| Editorial note: MiKo | |
| The material in this section is highly provisional | |
While the primary role of the MathML content element set is to directly encode the mathematical structure of expressions independent of the notation used to present the objects, rendering issues cannot be ignored. There are different approaches for rendering content MathML formulae, ranging from from native implementations of the K-14 element set over declarative notation definitions
| Editorial note: miko | |
| cite note here | |
to XSLT style sheets. The MathML 3 Recommendation will not make one of these normative, but only specify the default notations of the content MathML elements by way of examples.
| Editorial note: MiKo | |
| maybe it is best to distribute these sections into the sections where the elements are defined. | |
4.5.1 Numbers
The default rendering of a simple cn-tagged object is the same as for
the presentation element mn with some provision for overriding the
presentation of the PCDATA by providing explicit mn tags. This is
described in detail in Section 4.2.3 Numbers (cn).
4.5.2 Symbols and Identifiers
If the content of a ci or csymbol element is tagged using
presentation tags, that presentation is used. If no such tagging is supplied then
the PCDATA content is rendered as if it were the content
of an mi element. In particular if an application supports bidirectional
text rendering, then the rendering follows the Unicode bidirectional rendering.
4.5.3 Applications
If F is the rendering of f and Ai those of ai, then the default rendering of an application element of the form
<apply>f a1 ... an</apply>
is
<mrow>
F
<mo fence="true">(</mo>
A1
<mo separator="true">,</mo>
...
<mo separator="true">,</mo>
An
<mo fence="true">)</mo>
</mrow>4.5.4 Binders
If b, c, xi, c, and s render to B, C, Xi, C, and S, then the default rendering of a binding element of the form
<bind>b<bvar>x1 ... xn</bvar>S</bind>
is
<mrow> B x1 <mo separator="true">,</mo> ... <mo separator="true">,</mo> xn <mo separator="true">.</mo> S </mrow>
4.5.5 Attributions
The default rendering of a semantics element is the default rendering of
its first child: the annotation and annotation-xml are not
rendered. When a presentation MathML annotation is provided, a MathML renderer may
optionally use this information to render the MathML construct. This would typically
be the case when the first child is a MathML content construct and the annotation is
provided to give a preferred rendering differing from the default for the content
elements.
![{\left[{\mn{0}},{\mn{1}}\right]}](image/interval1-interval_cc-ex1.gif)
![{\left({\mn{0}},{\mn{1}}\right]}](image/interval1-interval_oc-ex1.gif)
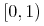

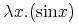
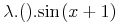
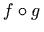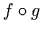
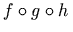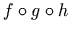
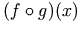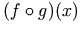
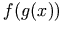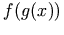
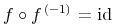
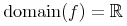
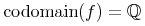

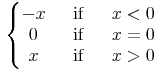
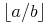
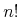
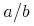
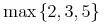
![{{\mo{\mathrm{max}}}{\left.\middle\{{{y}}\middle|{ {{y}\unicode{8712}{\left[{\mn{0}},{\mn{1}}\right]}} }\middle\}\right.}}](image/minmax1-big_max-ex1.gif)
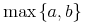

![{{\mo{\mathrm{min}}}{\left.\middle\{{{y}}\middle|{ {{y}\unicode{8712}{\left[{\mn{0}},{\mn{1}}\right]}} }\middle\}\right.}}](image/minmax1-big_min-ex1.gif)
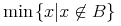
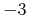
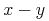
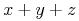
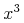

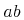
![\sqrt[{{{n}}}]{{a}}](image/arith1-root-ex1.gif)